Hướng dẫn giải Bài §1. Tập hợp. Phần tử của tập hợp, chương I – Ôn tập và bổ túc về số tự nhiên, sách giáo khoa toán 6 tập một. Nội dung bài giải bài 1 2 3 4 5 trang 6 sgk toán 6 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần số học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 6.
Lý thuyết
1. Định nghĩa
Tập hợp một hay nhiều đối tượng có tính chất đặc trưng giống nhau. Những đối tượng gọi là phần tử.
VD:
– Tập hợp các em học sinh lớp 61
– Tập hợp các số tự nhiên là bội số của 10 và nhỏ hơn 100
– Tập hợp các chữ cái a, b, c, d
2. Cách viết. Các ký hiệu
– Tên tập hợp được đặt bằng chữ cái in hoa.
VD:
A= { 0; 1; 2; 3 }
B= { a; b; c; d }
C= { x (in) N/ x<10}
– Các phần tử được viết trong 2 dấu {}
– Giữa các phần tử được ngăn cách bới dấu “,” hoặc dấu “;”
– Thứ tự các phần tử liệt kê tùy ý
– Mỗi phần tử được liệt kê một lần
– Có hai cách để viết 1 tập hợp là: Liệt kê các phần tử của tập hợp hay chỉ ra tính chất đặc trưng của các phần tử
VD: Viết tập hợp A các số tự nhiên chia 2 dư 1 và nhỏ hơn < 10
A={1,3,5,6,7}
A= {x (in) N/ x=2k+1; x<10}
Ký hiệu:
a (in) A đọc a là phần tử của tập hợp A hay phần tử a thuộc tập hợp A.
a (notin) A đọc a không là phần tử của tập hợp A hay phần tử a không thuộc tập hợp A.
– Một tập hợp có thể có một phần tử, có nhiều phần tử, có vô số phần tử, cũng có thể không có phần tử nào là tập hợp rỗng kí hiệu (emptyset).
– Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập hợp con của tập hợp B. Kí hiệu: A (subset) B đọc là: A là tập hợp con của tập hợp B hoặc A được chứa trong B hoặc B chứa A.
– Mỗi tập hợp đều là tập hợp con của chính nó và tập hợp rỗng là tập hợp con của mọi tập hợp.
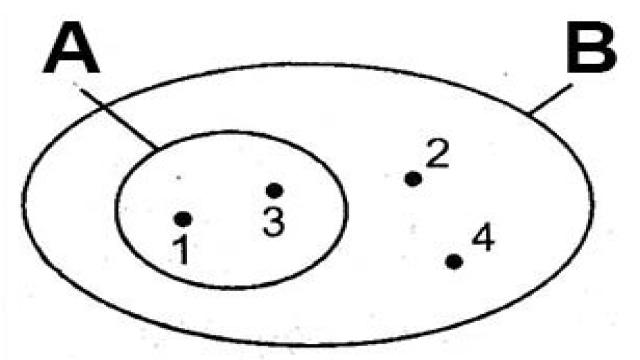
Cách tìm số tập hợp con của một tập hợp: Nếu A có n phần tử thì số tập hợp con của tập hợp A là 2n.
Dưới đây là phần trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!
Câu hỏi
1. Trả lời câu hỏi 1 trang 6 sgk Toán 6 tập 1
Viết tập hợp $D$ các số tự nhiên nhỏ hơn $7$ rồi điền kí hiệu thích hợp vào ô vuông: ( 2 ,square, D); (10 , square ,D)
Trả lời:
Tập hợp $D =$ {$0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6$}
Điền kí hiệu thích hợp: (2 in D;,,10 notin D).
2. Trả lời câu hỏi 2 trang 6 sgk Toán 6 tập 1
Viết tập hợp các chữ cái trong từ “NHA TRANG”.
Trả lời:
Các chữ cái trong từ “NHA TRANG” gồm $N, H, A, T, R, A, N, G$.
Trong các chữ cái trên, chữ $N$ được xuất hiện $2$ lần, chữ $A$ cũng được xuất hiện $2$ lần, nhưng ta chỉ viết mỗi chữ một lần, ta có tập hợp các chữ cái $A =$ {$N, H, A, T, R, G$}
Dưới đây là giải bài 1 2 3 4 5 trang 6 sgk toán 6 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần số học 6 kèm bài giải chi tiết bài 1 2 3 4 5 trang 6 sgk toán 6 tập 1 của bài §1. Tập hợp. Phần tử của tập hợp trong chương I – Ôn tập và bổ túc về số tự nhiên cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 1 trang 6 sgk Toán 6 tập 1
Viết tập hợp $A$ các số tự nhiên lớn hơn $8$ và nhỏ hơn $14$ bằng hai cách, sau đó điền kí hiệu thích hợp vào ô vuông:
$12 square A; 16 square A$
Bài giải:
Vì phần tử của $A$ là số tự nhiên lớn hơn $8$ và nhỏ hơn $14$ nên $8$ và $14$ không thuộc tập hợp $A$.
Nên $A = ${$9; 10; 11; 12; 13$}.
Dựa vào tính chất đặc trưng cho các phần tử $A =$ {$x in N, 8 < x < 14$}
Ta suy ra: $12 in A; 16 notin A.$
2. Giải bài 2 trang 6 sgk Toán 6 tập 1
Viết tập hợp các chữ cái trong từ “TOÁN HỌC”.
Bài giải:
Mỗi chữ cái trong “TOÁN HỌC” chỉ được liệt kê một lần, do đó tập hợp các chữ cái trong từ “TOÁN HỌC” là:
$A =$ {$T; O; A; N; H; O; C$}
3. Giải bài 3 trang 6 sgk Toán 6 tập 1
Cho hai tập hợp:
A = {a, b} ; B = {b, x, y}.
Điền kí hiệu thích hợp vào ô vuông:
$x square A ; y square B ; b square A ; b square B.$
Bài giải:
A = {a, b} suy ra tập A có 2 phần tử là: a, b
B = {b, x, y} suy ra tập B có 3 phần tử là: b, x, y
x (notin) A (Vì tập A có 2 phần tử là: a, b. Do đó x không thuộc tập A)
y ∈ B (Vì y là 1 phần tử của tập B)
b ∈ A (Vì b là 1 phần tử của tập A)
b ∈ B (Vì b là 1 phần tử của tập B)
4. Giải bài 4 trang 6 sgk Toán 6 tập 1
Nhìn các hình 3, 4 và 5, viết các tập hợp $A, B, M, H.$

Bài giải:
Mỗi đường cong kín biểu diễn một tập hợp, mỗi dấu chấm trong một đường cong kín biểu diễn một phần tử của tập hợp đó. Theo hình thì “bút” là một phần tử của tập hợp $H$.
Ta có: A = {15; 26}, B = {1; a; b}, M = {bút}, H = {sách; vở; bút}.
5. Giải bài 5 trang 6 sgk Toán 6 tập 1
a) Một năm gồm bốn quý. Viết tập hợp A các tháng của quý hai trong năm.
b) Viết tập hợp B các tháng (dương lịch) có 30 ngày.
Bài giải:
a) Vì mỗi quý có 3 tháng nên ta có A = {tháng tư; tháng năm; tháng sáu}
b) Phân tích: Xem các tháng trong năm theo thứ tự từ Tháng giêng đến Tháng 12, ta thấy Tháng 2 có 28 hoặc 29 ngày. Mỗi tháng còn lại đều gồm 30 hoặc 31 ngày. Tháng 7 và Tháng 8 đều có 31 ngày. Xen giữa hai tháng 31 ngày là một tháng có ít hơn 31 ngày.
Vậy B = {tháng 4; tháng 6; tháng 9; tháng 11}.
Bài tiếp theo:
- Giải bài 6 7 8 9 10 trang 7 8 sgk toán 6 tập 1
Xem thêm:
- Các bài toán 6 khác
- Để học tốt môn Vật lí lớp 6
- Để học tốt môn Sinh học lớp 6
- Để học tốt môn Ngữ văn lớp 6
- Để học tốt môn Lịch sử lớp 6
- Để học tốt môn Địa lí lớp 6
- Để học tốt môn Tiếng Anh lớp 6
- Để học tốt môn Tiếng Anh lớp 6 thí điểm
- Để học tốt môn Tin học lớp 6
- Để học tốt môn GDCD lớp 6
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 6 với giải bài 1 2 3 4 5 trang 6 sgk toán 6 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“
Chào mừng bạn đến với PRAIM, - nền tảng thông tin, hướng dẫn và kiến thức toàn diện hàng đầu! Chúng tôi cam kết mang đến cho bạn một trải nghiệm sâu sắc và tuyệt vời về kiến thức và cuộc sống. Với Praim, bạn sẽ luôn được cập nhật với những xu hướng, tin tức và kiến thức mới nhất.

















