Giải bài 1, 2, 3, 4 trang 6, bài 5 trang 7 SGK Toán lớp 8 tập 2 bài 1 Mở đầu về phương trình. Bài 3. Xét phương trình x + 1 = 1 + x. Ta thấy mọi số đều là nghiệm của nó. Người ta còn nói: Phương trình này nghiệm đúng với mọi x. Hãy cho biết tập nghiệm của phương trình đó.
Bài 1 trang 6 SGK Toán lớp 8 tập 2
Câu hỏi:
Với mỗi phương trình sau, hãy xét xem x = -1 có là nghiệm của nó không:
a) 4x – 1 = 3x – 2;
b) x + 1 = 2(x – 3);
c) 2(x + 1) + 3 = 2 – x
Phương pháp:
– Nếu khi thay (x = -1) vào hai vế của phương trình ta được kết quả của hai vế bằng nhau thì (x = -1) là nghiệm của phương trình đó.
Lời giải:
Thay giá trị x = -1 vào từng vế của phương trình, ta được:
a) Vế trái = 4x – 1 = 4(-1) – 1 = -5
Vế phải = 3x – 2 = 3(-1) – 2 = -5
Vế trái = Vế phải nên x = -1 là nghiệm của phương trình.
b) Vế trái = x + 1 = -1 + 1 = 0
Vế phải = 2(x – 3) = 2(-1 – 3) = -8
Vế trái ≠ Vế phải nên x = -1 không là nghiệm của phương trình.
c) Vế trái = 2(x + 1) + 3 = 2( -1 + 1) + 3 = 3
Vế phải = 2 – x = 2 – (-1) = 3
Vế trái = Vế phải nên x = -1 là nghiệm của phương trình.
Bài 2 trang 6 SGK Toán lớp 8 tập 2
Câu hỏi:
Trong các giá trị t = -1, t = 0 và t = 1, giá trị nào là nghiệm của phương trình: (t + 2)2 = 3t + 4?
Phương pháp:
Thay lần lượt các giá trị của t vào hai vế của phương trình ta được kết quả hai vế bằng nhau thì giá trị đó là nghiệm của phương trình.
Lời giải:
Lần lượt thay các giá trị của t vào hai vế của phương trình ta được:
– Tại t = -1 :
Vế trái = (t + 2)2 = (-1 + 2)2 = 1
Vế phải = 3t + 4 = 3.(-1) + 4 = 1
⇒ t = – 1 là nghiệm của phương trình (t + 2)2 = 3t + 4.
– Tại t = 0
Vế trái = (t + 2)2 = (0 + 2)2 = 4
Vế phải = 3t + 4 = 3.0 + 4 = 4
⇒ t = 0 là nghiệm của phương trình (t + 2)2 = 3t + 4.
– Tại t = 1
Vế trái = (t + 2)2 = (1 + 2)2 = 9
Vế phải = 3t + 4 = 3.1 + 4 = 7
⇒ t = 1 không là nghiệm của phương trình (t + 2)2 = 3t + 4.
Vậy t = -1, t = 0 là nghiệm của phương trình đã cho.
Bài 3 trang 6 SGK Toán lớp 8 tập 2
Câu hỏi:
Xét phương trình x + 1 = 1 + x. Ta thấy mọi số đều là nghiệm của nó. Người ta còn nói: Phương trình này nghiệm đúng với mọi x. Hãy cho biết tập nghiệm của phương trình đó.
Phương pháp:
Áp dụng định nghĩa:
– Nghiệm của phương trình là giá trị của ẩn (x) thoả mãn phương trình.
– Tập nghiệm của phương trình là tập hợp tất cả các nghiệm của phương trình đó.
Lời giải:
Vì phương trình (x + 1 = 1 + x) nghiệm đúng với mọi (x in mathbb R).
Vậy tập nghiệm của phương trình trên là: (S = mathbb R.)
Bài 4 trang 7 SGK Toán lớp 8 tập 2
Câu hỏi:
Nối mỗi phương trình sau với các nghiệm của nó:
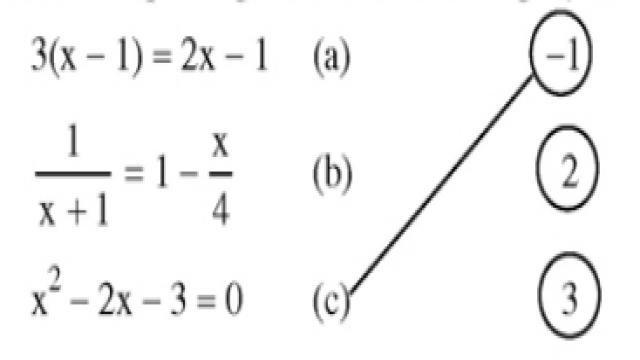
Lời giải:
*) Xét phương trình (3(x-1)=2x-1;;;;;(1))
+) Thay (x=-1) vào vế trái và vế phải của phương trình (1) ta được:
(eqalign{& VT = 3.left( { – 1 – 1} right) = 3.left( { – 2} right) = – 6 cr& VP = 2.left( { – 1} right) – 1 = – 2 – 1 = – 3 cr} )
( – 6 ne – 3 Rightarrow VT ne VP)
Vậy (x=-1) không là nghiệm của phương trình (1)
+) Thay (x=2) vào vế trái và vế phải của phương trình (1) ta được:
(eqalign{& VT = 3.left( {2 – 1} right) = 3.1 = 3 cr& VP = 2.2 – 1 = 4 – 1 = 3 cr} )
(3 = 3 Rightarrow VT = VP)
Vậy (x=2) là nghiệm của phương trình (1)
+) Thay (x=3) vào vế trái và vế phải của phương trình (1) ta được:
(eqalign{& VT = 3.left( {3 – 1} right) = 3.2 = 6 cr& VP = 2.3 – 1 = 6 – 1 = 5 cr} )
(6 ne 5 Rightarrow VT ne VP)
Vậy (x=3) không là nghiệm của phương trình (1)
*) Xét phương trình (dfrac{1}{{x + 1}} = 1 – dfrac{x}{4};;;;;(2))
+) Với (x=-1) thì phương trình (2) không xác định nên (x=-1) không là nghiệm của phương trình (2)
+) Thay (x=2) vào vế trái và vế phải của phương trình (2) ta được:
(eqalign{& VT = {1 over {2 + 1}} = {1 over 3} cr& VP = 1 – {2 over 4} = 1 – {1 over 2} = {1 over 2} cr} )
(dfrac{1}{3} ne dfrac{1}{2} Rightarrow VT ne VP)
Vậy (x=2) không là nghiệm của phương trình (2)
+) Thay (x=3) vào vế trái và vế phải của phương trình (2) ta được:
(eqalign{& VT = {1 over {3 + 1}} = {1 over 4} cr& VP = 1 – {3 over 4} = {4 over 4} – {3 over 4} = {1 over 4} cr} )
(dfrac{1}{4} = dfrac{1}{4} Rightarrow VT = VP)
Vậy (x=3) là nghiệm của phương trình (2)
*) Xét phương trình ({x^2} – 2x – 3 = 0,,,,,,,,,,,,,(3))
+) Thay (x=-1) vào vế trái và vế phải của phương trình (3) ta được:
(eqalign{& VT = {left( { – 1} right)^2} – 2.left( { – 1} right) – 3cr&;;;;;;; = 1 + 2 – 3 = 0 cr& VP = 0 cr} )
(0 = 0 Rightarrow VT = VP)
Vậy (x=-1) là nghiệm của phương trình (3)
+) Thay (x=2) vào vế trái và vế phải của phương trình (3) ta được:
(eqalign{& VT = {2^2} – 2.2 – 3 = 4 – 4 – 3 = – 3 cr& VP = 0 cr} )
( – 3 ne 0 Rightarrow VT ne VP)
Vậy (x=2) không là nghiệm của phương trình (3)
+) Thay (x=3) vào vế trái và vế phải của phương trình (3) ta được:
(eqalign{& VT = {3^2} – 2.3 – 3 = 9 – 6 – 3 = 0 cr& VP = 0 cr} )
(0 = 0 Rightarrow VT = VP)
Vậy (x=3) là nghiệm của phương trình (3)
Ta nối như sau:
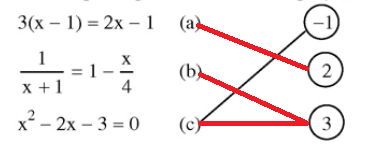
Bài 5 trang 7 SGK Toán lớp 8 tập 2
Câu hỏi:
Hai phương trình x = 0 và x(x – 1) = 0 có tương đương không? Vì sao?
Lời giải:
Phương trình (x = 0) có tập nghiệm ({S_1} = {rm{{ }}0} ).
Xét phương trình (x(x – 1) = 0).
Ta có một tích bằng (0) khi một trong hai thừa số bằng (0) tức là:
(x(x – 1) = 0) khi (x = 0) hoặc (x = 1).
Vậy phương trình (x(x – 1) = 0) có tập nghiệm ({S_2} = {rm{{ }}0;1} )
Vì ({S_1} ne {S_2}) nên hai phương trình không tương đương.
Sachbaitap.com
Bài tiếp theo
Chào mừng bạn đến với PRAIM, - nền tảng thông tin, hướng dẫn và kiến thức toàn diện hàng đầu! Chúng tôi cam kết mang đến cho bạn một trải nghiệm sâu sắc và tuyệt vời về kiến thức và cuộc sống. Với Praim, bạn sẽ luôn được cập nhật với những xu hướng, tin tức và kiến thức mới nhất.

















