Đường Tròn Lượng Giác: Những Bí Mật Bên Trong

Đường tròn lượng giác là một chủ đề quan trọng trong toán học. Nó liên quan đến cung và góc lượng giác trên đường tròn. Hôm nay, tôi sẽ chia sẻ với các bạn những bí mật thú vị xoay quanh đề tài này.

Khái Niệm Chung về Cung và Góc Lượng Giác

Cung Lượng Giác là Gì?

Đầu tiên, chúng ta cần hiểu khái niệm về cung lượng giác. Một đường tròn có bán kính R và tâm O. Trên đường tròn đó, chúng ta có hai điểm A và B. Khi đó, chúng ta gọi $widehat{AmB}$ là cung nhỏ và $widehat{AnB}$ là cung lớn. Khi viết $widehat{AB}$, chúng ta hiểu đó là cung nhỏ và AB là dây cung chắn cung $widehat{AB}$.

Góc Lượng Giác là Gì?

Góc lượng giác là khi chúng ta có hai góc có cùng tia đầu và tia cuối nhưng có các số đo khác nhau một bội nguyên $360^{circ}$ (hay $2pi$).

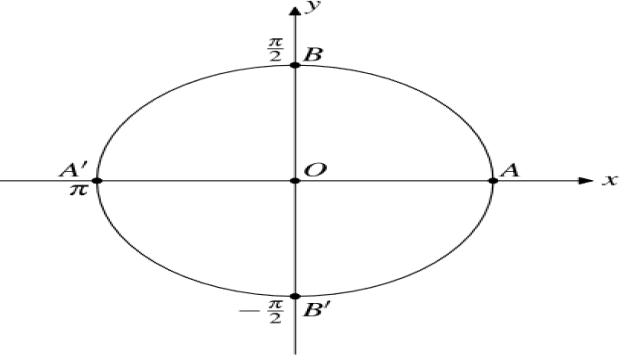
Trên đường tròn lượng giác, chúng ta vẽ đường tròn tâm O, bán kính R. Đồng thời, chúng ta chọn điểm A làm gốc và chọn chiều quay ngược với chiều kim đồng hồ là chiều dương. Điểm M(x;y) trên đường tròn lượng giác có cung lượng giác có số đo α được gọi là điểm trên đường tròn lượng giác biểu diễn cung lượng giác.

Đơn Vị Đo Cung và Góc Lượng Giác

Đơn Vị Radian

Radian là đơn vị đo cung trên đường tròn có độ dài chính bằng bán kính R của đường tròn. Đơn vị này được kí hiệu là rad hoặc có thể bỏ rad và kí hiệu là 1.

Đơn Vị Độ

Độ là đơn vị đo góc, được tính bằng $frac{1}{180}$ góc bẹt. Kí hiệu là 1o và có giá trị là 60.

Đổi Độ ra Radian

Để đổi độ ra radian, chúng ta áp dụng công thức sau:

Độ Dài của Một Cung Tròn

Độ dài của một cung trên đường tròn được tính theo công thức:

Bảng Giá Trị Lượng Giác

Trong toán học, có một số giá trị lượng giác quan trọng mà chúng ta cần biết. Dưới đây là một số công thức tính giá trị lượng giác của các góc:

Một Số Bài Tập về Các Dạng Toán Cung và Góc Lượng Giác

Cuối cùng, chúng ta sẽ thực hành qua một số bài tập về các dạng toán liên quan đến cung và góc lượng giác.

Cung Lượng Giác Trên Đường Tròn Được Biểu Diễn Thế Nào?

Ví dụ 1: Tính giá trị biểu thức lượng giác:

1. $sin(frac{3pi}{2})$
2. $cos(frac{pi}{2})$

Cách giải:

1. Ta có: $sin(frac{3pi}{2}) = sin(pi + frac{pi}{2})$. Ta chia đường tròn thành tám phần bằng nhau. Khi đó, điểm M là điểm biểu diễn góc có số đo $frac{pi}{2}$.
2. Ta có: $cos(frac{pi}{2}) = cos(pi + frac{pi}{2})$. Khi đó, điểm M’ là điểm biểu diễn góc trùng với góc $frac{pi}{2}$.

Cách Xác Định Giá Trị Của Biểu Thức Chứa Góc Đặc Biệt

Ví dụ 2: Cho $tan(x) = -1$. Xác định dấu của các giá trị lượng giác:

1. $cos(x)$
2. $sin(x)$
3. $csc(x)$

Cách giải:

1. Chúng ta có: $tan(x) = frac{sin(x)}{cos(x)} = -1$. Vì $tan(x)$ là âm và $sin(x) = cos(x)$, nên giá trị của $cos(x)$ là âm.
2. Tương tự như trên, giá trị của $sin(x)$ cũng là âm.
3. Do $sin(x)$ là âm, nên $csc(x)$ sẽ là số âm.

Chứng Minh Biểu Thức Không Phụ Thuộc Góc X, Đơn Giản Biểu Thức

Ví dụ 3: Chứng minh $sin^2(x) + cos^2(x) = 1$.

Cách giải:

• Ta sử dụng các hằng đẳng thức $sin^2(x) + cos^2(x) = 1$ và các hệ thức lượng giác cơ bản.
• Vì đã có đẳng thức ban đầu, chúng ta có thể biến đổi hai vế của đẳng thức sao cho bằng nhau hoặc biến đổi chúng cùng với một số lượng giác khác.

Tôi hy vọng qua bài viết này, các bạn đã hiểu thêm về đường tròn lượng giác và các bí mật xung quanh nó. Để nắm vững kiến thức này, hãy truy cập PRAIM để đăng ký tài khoản và ôn tập thêm nhiều bài tập về lượng giác nhé!