Định lý pytago – toán 7 là một trong những kiến thức vô cùng quan trọng. Nó là nền tảng để các em giải quyết các bài tập phức tạp sau này. Do đó, hãy tập trung học và ghi chú bài vở thật cẩn thận nha. Hôm nay, các em sẽ cùng với itoan tìm hiểu về Định lý Pytago và cách tính cạnh tam giác còn lại khi biết số đo của 2 cạnh của 1 tam giác vuông.
Mục tiêu bài học Định lý pytago
- Nắm chắc và hiểu lý thuyết, cũng như các ví dụ trong bài học Định lý Pytago
- Hiểu cách dùng định lý Pytago.
- Hoàn thành các bài tập trong sách giáo khoa và bài tập tự luyện để củng cố kiến thức.
Lý thuyết cần nhớ bài Định lý pytago
1. Định lý pytago là gì?
Định lý Pytago (hay còn gọi là định lý Pythagoras theo tiếng Anh) là một liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông. Định lý pytago thuận phát biểu rằng trong 1 tam giác vuông: Bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc vuông.
Định lý có thể viết thành một phương trình liên hệ giữa độ dài của các cạnh là a, b và c, thường gọi là công thức Pytago
(trong đó c độ dài là cạnh huyền, a,b lần lượt là độ dài 2 cạnh góc vuông)
2. Ví dụ bài tập:
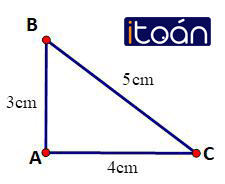
Cho tam giác ABC vuông tại A có AB= 6cm, AC= 8cm. Tính BC
Áp dụng định lý Pitago trong tam giác vuông ABC, ta có: BC2=AB2+AC2
Nên BC2=62+82=36+64=100
Vậy BC=10 cm
Chú ý: Dựa vào định Pytago, khi ta biết độ dài 2 cạnh của tam giác vuông, ta sẽ tính được độ dài cạnh còn lại
3. Cách chứng minh định lý pitago lớp 7
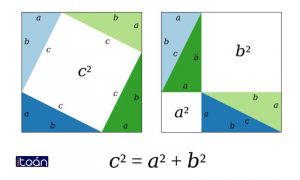
Ta có thể chứng minh định lý Pytago đơn giản qua hình dưới đây:
Ở hình trên ta có 2 hình vuông lớn có diện tích bằng nhau là: (a+b)2
Trong mỗi hình lại có 4 tam giác vuông bằng nhau có diện băng nhau là 1/2(a.b). Do đó diện tích khoảng trắng của 2 hình sẽ bằng nhau.
Như vậy, diện tích của hình vuông c sẽ bằng tổng diện tích của 2 hình vuông a và b nên ta có: c2=a2+b2
4. Chức minh định lý Pytago đảo
Định nghĩa: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông.
Định lý Pytago đảo được sử dụng rất phổ biến cũng như gồm nhiều ứng dụng trong thực tiễn. Đây là một định lý toán học quan trọng hàng đầu của hình học cơ bản.
Ví dụ: Tam giác ABC có BC2=AB2+AC2 => tam giác ABC bằng 90o
Để hiểu hơn về bài học ngày hôm nay, các em hãy theo dõi video bài giảng dưới đây nhé!
Bài tập SGK Định lý pytago Toán 7
Trả lời câu hỏi Toán 7 Tập 1 Bài 7 trang 129:
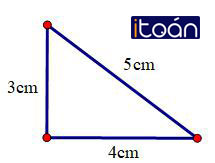
Vẽ một tam giác vuông có các cạnh góc vuông bằng 3cm và 4cm. Đo độ dài cạnh huyền
Hướng dẫn giải bài tập:
Đo được cạnh huyền 5cm
Trả lời câu hỏi Toán 7 Tập 1 Bài 7 trang 129:
Lấy giấy trắng cắt tám tam giác vuông bằng nhau. Trong mỗi tam giác vuông đó, ta gọi độ dài các cạnh góc vuông là a và b, gọi độ dài cạnh huyền là c. Cắt hai tấm bìa hình vuông có cạnh bằng a+b
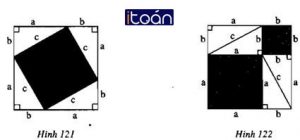
a) Đặt bốn tam giác vuông lên tấm bìa hình vuông như hình 121. Phần bìa không bị che lấp là một hình vuông có cạnh bằng c, tính diện tích phần bìa đó theo c
b) Đặt bốn tam giác vuông còn lại lên tấm bìa hình vuông thứ hai như hình 122. Phần bìa không bị che lấp gồm hai hình vuông có cạnh là a và b; tính diện tích phần bìa đó theo a và b
c) từ đó rút ra nhận xét gì về quan hệ giữa c2 và a2 + b2?
Hướng dẫn giải bài tập:
a) diện tích phần bìa hình vuông cạnh c là c2
b) diện tích hai phần bìa hình vuông lần lượt là a2 và b2
c) nhận xét c2 = a2 + b2
Trả lời câu hỏi Toán 7 Tập 1 Bài 7 trang 130:
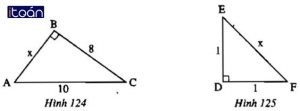
Tìm độ dài x trên các hình 124, 125
Hướng dẫn giải bài tập:
Áp dụng định lí Py – ta – go
Tam giác ABC vuông tại B
⇒ x2 + 82 = 102
⇒ x2 = 102 – 82 = 36
⇒ x = 6 (cm)
Tam giác DEF vuông tại D
⇒ 12 + 12 = x2
⇒ x2 = 1 + 1 = 2
⇒ x = √2 (cm)
Trả lời câu hỏi Toán 7 Tập 1 Bài 7 trang 130:
Vẽ tam giác ABC có AB = 3cm; AC = 4cm; BC = 5cm. Hãy dùng thước đo góc để xác định số đo của góc BAC
Hướng dẫn giải bài tập:
Số đo góc BAC là 90o
Bài 53 (trang 131 SGK Toán 7 Tập 1):
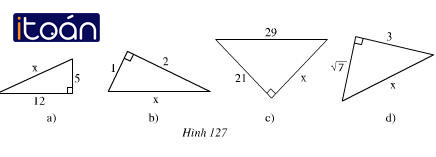
Tìm độ dài x trên hình 127.
Hướng dẫn giải bài tập:
a) Hình a
Áp dụng định lí Pi-ta-go ta có:
x2 = 122 + 52 = 144 + 25 = 169 => x = 13
b) Hình b
Ta có: x2 = 12 + 22 = 1 + 4 = 5
=> x = √5
c) Hình c
Theo định lí Pi-ta-go 292 = 212 + x2
Nên x2 = 292 – 212 = 841 – 441 = 400
=> x = 20
d) Hình d
Theo định lí Pi-ta-go: 7 + 32 = x2
=> x2 = 16 => x = 4
Bài 54 (trang 131 SGK Toán 7 Tập 1):
Đoạn lên dốc từ C đến A dài 8,5m, độ dài CB bằng 7,5m. Tính chiều cao AB.
Hướng dẫn giải bài tập:
Áp dụng định lí Pi-ta-go trong ΔABC ta có:
AB2 + BC2 = AC2
=> AB2 = AC2 – BC2 = 8,52 – 7,52
= 72,25 – 56,25 = 16
Vậy AB = 4(cm)
Bài 55 (trang 131 SGK Toán 7 Tập 1):
Tính chiều cao của bức tường, biết rằng chiều dài của thang là 4m và chân thang cách tường 1m.
Hướng dẫn giải bài tập:
Kí hiệu như hình vẽ:
Áp dụng định lí Pi-ta-go trong ΔABC ta có:
AC2 + BC2 = AB2
=> AC2 = AB2 – BC2 = 16 – 1 = 15
=> AC = √15 = 3,87(m) hay chiều cao của bức tường là 3,87m.
Bài 56 (trang 131 SGK Toán 7 Tập 1):
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau.
a) 9cm, 15cm, 12cm.
b) 5dm, 13dm, 12dm.
c) 7m, 7m, 10m.
Hướng dẫn giải bài tập:
a) Ta có: 152= 225 = 92+ 122 = 81 + 144
Nên tam giác có độ dài 9cm, 12cm, 15cm là tam giác vuông
b) Tương tự là tam giác vuông (vì 52+ 122= 132)
c) Không là tam giác vuông (vì 72+ 72< 102)
Bài 57 (trang 131 SGK Toán 7 Tập 1):
Cho bài toán “ΔABC có AB = 8, AC = 17, BC = 15 có phải là tam giác vuông hay không? Bạn Tâm đã giải thích bài toán đó như sau:
AB2 + AC2 = 82 + 172 = 64 + 289 = 353
BC2 = 152 = 225
Vì 353 ≠ 225 nên AB2 + AC2 ≠ BC2
Vậy ΔABC không phải là tam giác vuông.”
Lời giải trên đúng hay sai? Nếu sai hãy sửa lại cho đúng
Hướng dẫn giải bài tập:
Lời giải của bạn Tâm sai. Sửa lại như sau:
Ta có AC2 = 172 = 289 = AB2 + BC2 = 82 + 152
Vậy ΔABC là tam giác vuông.
(Lưu ý: Từ bài toán trên, để xác định xem một tam giác có phải là tam giác vuông không, ta cần so sánh tổng bình phương số đo của hai cạnh bé với bình phương của cạnh có số đo lớn nhất.)
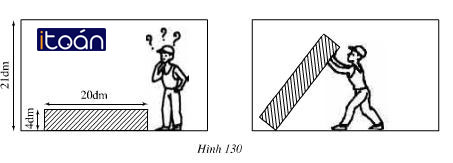
Bài 58 (trang 132 SGK Toán 7 Tập 1):
Đố. Trong lúc anh Nam dựng tủ cho đứng thẳng, tủ có bị vướng vào trần nhà không?
Hướng dẫn giải bài tập:
Gọi d là đường chéo của tủ.
Ta có d2 = 202 + 42 = 400 + 16 = 416
=> d = √416 = 20,4 dm
Suy ra d < 21dm (là chiều cao của căn phòng)
Như vậy khi anh Nam đẩy tủ cho đứng thẳng tủ không bị vướng vào trần nhà
Bài 59 (trang 133 SGK Toán 7 Tập 1):
Bạn Tâm muốn đóng một nẹp chéo AC để chiếc khung hình chữ nhật ABCD được vững hơn. Tính độ dài AC, biết rằng AD = 48cm, CD = 36cm.
Hướng dẫn giải bài tập:
Áp dụng định lí Pi-ta-go trong ΔACD ta có:
AC2 = AD2 + CD2 = 482 + 362 = 2304 + 1296 = 3600
=> AC = 60(cm)
Bài 60 (trang 133 SGK Toán 7 Tập 1):
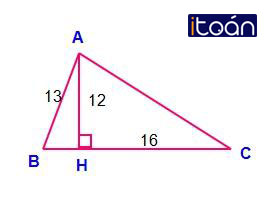
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC. Cho biết AB = 13cm, AH = 12cm, HC = 16cm. Tính độ dài AC, BC.
Hướng dẫn giải bài tập:
Áp dụng định lí Pi-ta-go trong ΔAHC ta có:
AC2 = AH2 + HC2 = 122 + 162 = 144 + 256 = 400
=> AC = 20 (cm)
Áp dụng định lí Pi-ta-go trong ΔAHB ta có:
BH2 = AB2 – AH2 = 132 – 122 = 169 -144 = 25
=> BH = 5cm
Do đó BC = BH + HC = 5 + 16 = 21 (cm)
Bài 61 (trang 133 SGK Toán 7 Tập 1):
Trên giấy kẻ ô vuông (độ dài cạnh của ô vuông bằng 1) cho tam giác ABC như hình 135. Tính độ dài mỗi cạnh của tam giác.
Hướng dẫn giải bài tập:
Áp dụng định lí Pi-ta-go trong ΔAMB ta có:
AB2 = AM2 + MB2 = 22 + 12 = 5
=> AB = √5
Áp dụng định lí Pi-ta-go trong ΔANC ta có:
AC2 = AN2 + NC2 = 32 + 42 = 25
=> AC = 5
Áp dụng định lí Pi-ta-go trong ΔBKC ta có:
BC2 = BK2 + KC2 = 32 + 52 = 34
=> BC = √34
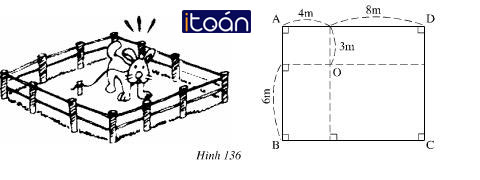
Bài 62 (trang 133 SGK Toán 7 Tập 1):
Đố. Người ta buộc con cún bằng sợi dây có một đầu dây buộc tại điểm O làm cho con Cún cách điểm O nhiều nhất 9m. Con Cún có thể tới các vị trí A, B, C, D để canh giữ mảnh vườn hình chữ nhật ABCD hay không?
Hướng dẫn giải bài tập:
Ta có: OA2 = 42 + 32 = 16 + 9 = 25
=> OA = 5m < 9m
OC2 = 62 + 82 = 36 + 64 = 100
=> OC = 10m > 9m
OB2 = 42 + 62 = 16 + 36 = 52
=> OB = √52m < 9m
OD2 = 32 + 82 = 9 + 64 = 73
=> OD = √73 < 9m
Vì con Cún chỉ tới được vị trí xa nhất cách O là 9m nên như vậy con Cún có thể tới các vị trí A, B, D nhưng không tới được vị trí C.
Bài tập tự luyện Định lý pytago
Bài tập 1: Cho tam giác nhọn ABC, kẻ AH vuông góc với BC ( H ∈ BC). CHo biết AH=12cm, BH=5cm và BC=14cm. Tính các độ dài AB và AC.
A. AB= 14cm; AC= 15cm
B. AB= 13cm; AC= 15cm
C. AB= 15cm, AC= 16cm
D. Một kết quả khác với ba kết quả trên
Bài tập 2: Cho tam giác ABC vuông cân tại A. Tính độ dài cạnh BC biết AB = AC = 2dm
A. BC = 4dm
B. BC = √6dm
C. BC = 8dm
D. BC = √8 dm
Bài tập 3: Một tam giác vuông có cạnh huyền bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông?
A. 10 cm, 22 cm
B. 10 cm, 24 cm
C. 12 cm, 24 cm
D. 15 cm, 24 cm
Bài tập 4: Cho tam giác ABC vuông tại B BC=12cm, AC=13cm. Tính AB
A. x = 10cm
B. x = 11cm
C. x = 8cm
D. x = 5cm
Bài tập 5: Cho tam giác MNP vuông tại M, MN=4,5cm, NP =7,5cm. TInh độ dài MP
A. 5,5cm
B. 7,5cm
C. 4,5cm
D. 6cm
Hướng dẫn giải bài tập tự luyện Định lý pytago
Bài tập 1: B
Bài tập 2: D
Bài tập 3: B
Bài tập 4: D
Bài tập 5: A
Lời kết
Vậy là bài học về định lý Pytago đã kết thúc tại đây. Mặc dù bài học tuy không dài nhưng các em hãy tập trung ghi chú cẩn thận nhé, vì các em sẽ còn gặp kiến thức này rất nhiều lần ở các lớp cao hơn. itoan chúc các em học thật tốt và gặt hái được nhiều điểm cao.
Xem thêm bài giảng tại đây:
- Từ vuông góc đến song song – Lý thuyết và Bài tập SGK Toán 7
- Đơn thức đồng dạng – Học toán đại số 7 cùng iToan
- Trường hợp bằng nhau thứ nhất của tam giác cạnh cạnh cạnh
Chào mừng bạn đến với PRAIM, - nền tảng thông tin, hướng dẫn và kiến thức toàn diện hàng đầu! Chúng tôi cam kết mang đến cho bạn một trải nghiệm sâu sắc và tuyệt vời về kiến thức và cuộc sống. Với Praim, bạn sẽ luôn được cập nhật với những xu hướng, tin tức và kiến thức mới nhất.