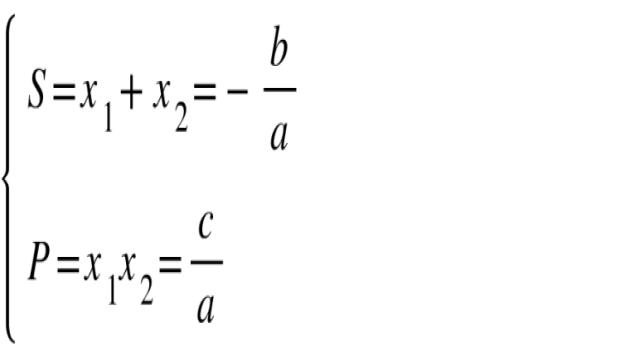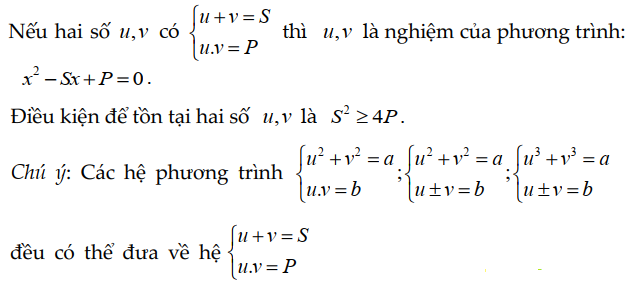Học cách sử dụng các dạng bài toán hệ thức Viet

Hệ thức Viet là một phần kiến thức cực kỳ quan trọng trong Toán cấp THCS và chương trình học Toán 9. Nó thường xuất hiện trong các cuộc thi học sinh giỏi và kỳ thi tuyển sinh vào lớp 10. Cùng PRAIM tìm hiểu về các dạng bài hệ thức Viet và ví dụ giải thích, để các bạn học sinh có thể tham khảo và áp dụng vào việc giải các bài toán.

I. Lý thuyết quan trọng về Hệ thức Viet

Hệ thức Viet hay định lý Viet được một nhà toán học người Pháp – François Viète tìm ra. Định lý này thể hiện mối quan hệ giữa các nghiệm trong một phương trình đa thức. Gồm Định lý Viet thuận, Hệ thức Viet ngược và Hệ thức Viet đảo.

1. Hệ thức Viet thuận

Cho phương trình bậc hai một ẩn: ax^2 + bx + c = 0 (a ≠ 0) có 2 nghiệm x1 và x2. Khi đó, 2 nghiệm x1, x2 thỏa mãn hệ thức sau:

Hệ quả: Dựa vào hệ thức Viet, ta có thể nhẩm luôn nghiệm của phương trình trong một số trường hợp đặc biệt khi phương trình bậc 2 một ẩn có nghiệm.

2. Hệ thức Viet đảo

Giả sử hai số thực x1, x2 thỏa mãn hệ thức:

Chú ý: S^2 – 4P ≥ 0 là điều kiện bắt buộc để phương trình bậc hai tồn tại 2 nghiệm là x1 và x2.

II. Các dạng bài tập hệ thức Viet (có kèm ví dụ)

Sau khi bạn đã nắm được những kiến thức quan trọng, tiếp theo chúng ta sẽ cùng tìm hiểu về các dạng bài tập hệ thức Viet hay gặp.

Dạng 1: Tính nhẩm nghiệm dựa vào hệ thức Viet

Khi giải các bài toán giải phương trình bậc 2, chúng ta thường sử dụng biệt thức Δ để suy ra các nghiệm x1, x2 (nếu có). Tuy nhiên bạn có thể dễ dàng tính nhẩm nhanh hơn nhờ hệ thức Viet. (Áp dụng hệ quả của hệ thức Viet thuận ở phần I)

Nhận xét: Qua 2 ví dụ, phương pháp này có thể giúp bạn giải các phương trình đặc biệt trở nên dễ dàng và nhanh chóng.

Dạng 2. Tìm giá trị của biểu thức giữa các nghiệm

Nếu phương trình ax^2 + bx + c = 0 ( a ≠ 0) có hai nghiệm x1 và x2, ta có thể thể hiện các biểu thức đối xứng giữa các nghiệm theo S = x1 + x2 và P = x1.x2.

Chú ý: Khi tìm giá trị một biểu thức giữa các nghiệm thông thường, ta phải biến đổi sao cho xuất hiện tổng và tích các nghiệm trong biểu thức đó rồi áp dụng định lý Viet.

Dạng 3: Tìm hai số sau khi biết tổng và tích

Theo hệ thức Vi-ét, ta có:

Ví dụ: Cho hình chữ nhật ABCD với diện tích và chu vi lần lượt là 2a2 và 6a. Hãy tìm các kích thước của hình chữ nhật.

Lời giải:

Gọi x, y lần lượt là các kích thước của hình chữ nhật ABCD ( x, y > 0)

…

Dạng 4: Ứng dụng phân tích tam thức bậc hai thành nhân tử

Thí dụ ta có: ax^2 + bx + c = 0 có Δ ≥ 0 ( a ≠ 0)

…

Dạng 5. Tìm ĐK của tham số để phương trình bậc 2 có một nghiệm x = x1 cho trước. Tìm nghiệm thứ hai

Tìm ĐK để phương trình có nghiệm x = x1 cho trước là một trong những dạng bài tập phổ biến. Có 2 cách tìm ĐK để phương trình có nghiệm x = x1:

Cách 1:

1. Tìm điều kiện để phương trình có hai nghiệm (Điều kiện ).
2. Tìm giá trị của tham số bằng cách thay x = x1 vào phương trình.
3. Đối chiếu giá trị tham số vừa tìm được với điều kiện (Δ ≥ 0) và kết luận

Cách 2:

1. Thay x = x1 vào phương trình đã cho để tìm giá trị của tham số.
2. Thay giá trị tham số vừa tìm được vào phương trình và giải.

Chú ý: Nếu Δ < 0 sau khi thay giá trị của tham số vào phương trình đã cho => Kết luận: Không có giá trị nào của tham số để phương trình có nghiệm x1 cho trước.

Tìm nghiệm thứ hai

Sau khi tìm được điều kiện, chúng ta sẽ tiến hành tìm nghiệm thứ hai bằng 3 cách:

Cách 1: Thay giá trị của tham số vừa tìm được rồi giải phương trình.
Cách 2: Thay giá trị của tham số vừa tìm được vào công thức tổng 2 nghiệm => nghiệm thứ 2.
Cách 3: Thay giá trị của tham số vừa tìm được vào công thức tích hai nghiệm => nghiệm thứ 2.

Ví dụ: Với giá trị k nào thì:

a) Phương trình 2x^2 + kx – 10 = 0 có một nghiệm x = 2. Tìm nghiệm kia?
b) Phương trình (k – 5)x^2 – (k – 2)x + 2k = 0 có một nghiệm x = – 2. Tìm nghiệm kia?
c) Phương trình kx^2 – kx – 72 có một nghiệm x = – 3. Tìm nghiệm kia?

…

Các dạng bài tập hệ thức Viet còn rất nhiều và đa dạng. PRAIM hy vọng qua bài viết này, các bạn học sinh đã có cái nhìn tổng quan về cách áp dụng hệ thức Viet trong việc giải các bài toán. Hãy ôn tập kỹ kiến thức và thực hành làm các bài tập để nắm vững hơn. PRAIM luôn đồng hành cùng bạn trên con đường học tập. Nếu bạn cần thêm thông tin hoặc muốn tìm hiểu thêm về chương trình học Toán, hãy truy cập PRAIM.