Đề thi tuyển sinh lớp 10 năm 2023-2024 Đồng Nai môn Toán – Kỳ thi vào lớp 10 năm 2023 của tỉnh Đồng Nai đã cận kề. Để tiện cho các em học sinh có thêm tài liệu so sánh và đối chiếu với kết quả bài làm sau khi kì thi kết thúc. Trong bài viết này Hoatieu xin chia sẻ đề thi tuyển sinh lớp 10 môn Toán Đồng Nai 2023-2024 cùng với đáp án đề thi vào 10 môn Toán Đồng Nai 2023, mời các bạn cùng tham khảo.
- Đáp án đề thi tuyển sinh lớp 10 môn Văn Đồng Nai 2023
Theo đó, kì thi vào lớp 10 năm 2023 tỉnh Đồng Nai sẽ chính thức diễn ra trong 2 ngày: 2 và 3-6 với 3 môn thi bắt buộc là Toán, Văn, tiếng Anh. Các thí sinh thi vào chuyên Lương Thế Vinh sẽ thi môn chuyên tương ứng.
Lưu ý: Đáp án đề thi tuyển sinh lớp 10 môn Toán Đồng Nai 2023 sẽ được Hoatieu cập nhật ngay sau khi kì thi kết thúc.
1. Đáp án đề thi tuyển sinh lớp 10 môn Toán 2023 Đồng Nai
Đáp án đề thi vào lớp 10 môn Toán Đồng Nai đang được các thầy cô giải. Các em mở sẵn bài viết, chờ 1 lúc rồi nhấn F5 để xem đáp án.
2. Đề thi tuyển sinh lớp 10 môn Toán 2023 Đồng Nai
3. Lịch thi vào lớp 10 năm 2023 Đồng Nai
Ngày 1/3, Sở GD-ĐT Đồng Nai cho biết, đơn vị đã ban hành hướng dẫn thi tuyển sinh lớp 10 năm học 2023-2024. Theo đó, kỳ thi tuyển sinh vào lớp 10 năm nay sẽ diễn ra vào các ngày 2/6 và 3/6.
Cụ thể, học sinh vẫn thi 3 môn Toán, Ngữ văn (mỗi môn 120 phút) và môn Tiếng Anh (60 phút), riêng các thí sinh thi vào lớp chuyên Trường THPT chuyên Lương Thế Vinh sẽ thi thêm môn chuyên tương ứng (150 phút).
So với các kỳ thi năm trước, nội dung kiến thức trong chương trình toàn cấp THCS do Bộ GD-ĐT ban hành, chủ yếu là chương trình lớp 9.
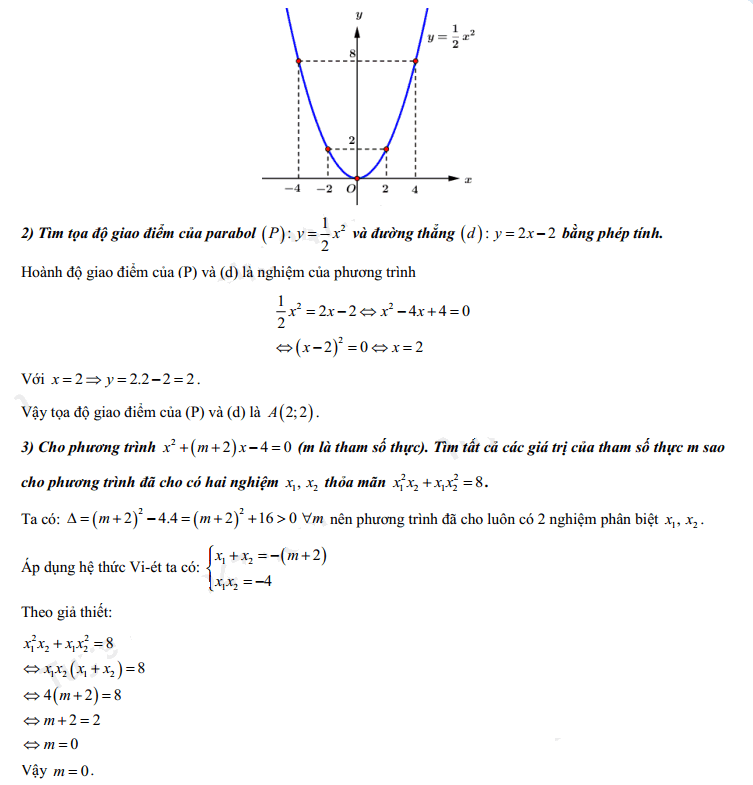
4. Đáp án đề thi vào 10 2022 môn Toán Đồng Nai
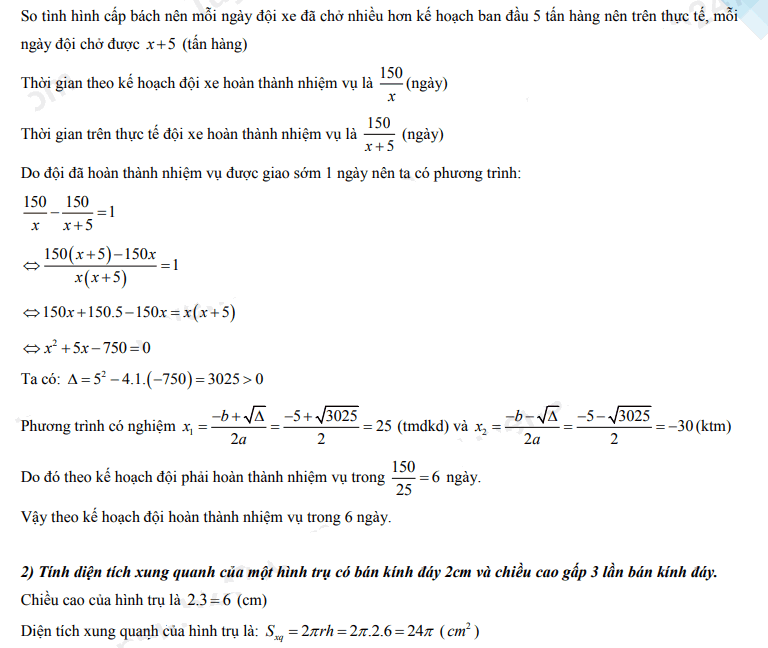
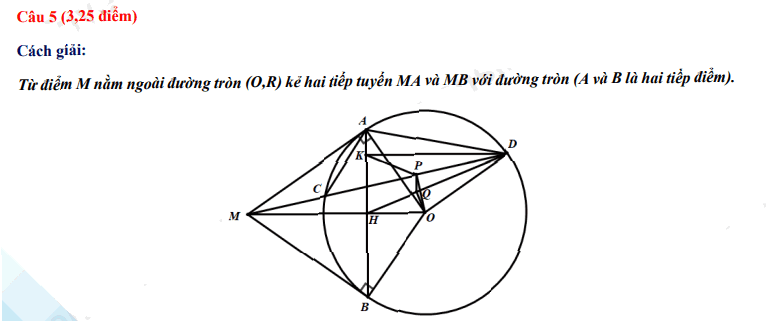
5. Đề thi tuyển sinh lớp 10 2022 Đồng Nai môn Toán
6. Đề thi vào lớp 10 năm 2021 môn Toán tỉnh Đồng Nai
7. Đáp án đề thi vào lớp 10 năm 2021 môn Toán tỉnh Đồng Nai
Câu 1: (2 điểm)
1) Giải phương trinh 
Ta có: 
0″ width=”228″ height=”24″ data-latex=”Delta=3^{2}-4 cdot(-10)=49>0″ data-i=”1″ class=”lazy” data-src=”https://tex.vdoc.vn/?tex=%5CDelta%3D3%5E%7B2%7D-4%20%5Ccdot(-10)%3D49%3E0″> nên phương trình có 2 nghiệm phân biệt 
Vậy tập nghiệm của bất phương trình là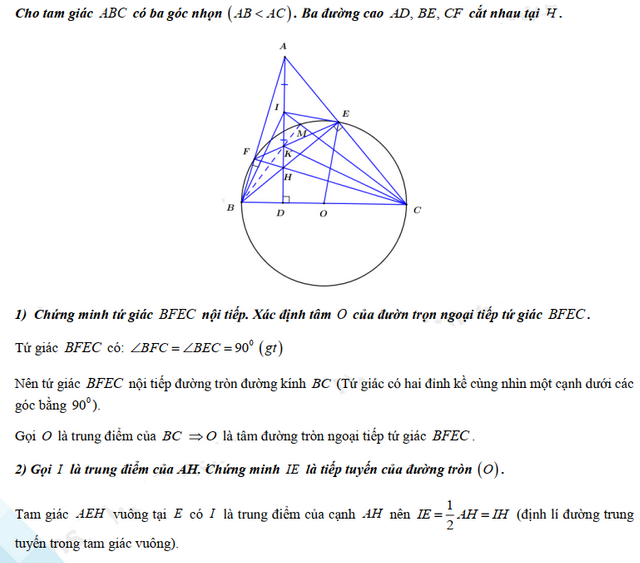 
.
2) Giải phương trình 
Đặt , phương trình đã cho trở thành .
Ta có nên phương trình có 2 nghiệm phân biệt .
Với .
Vậy tập nghiệm của phương trình .
3) Giải hệ phương trình
Ta có:
Vậy hệ phương trình có nghiệm .
Câu 2: (2,25 điểm)
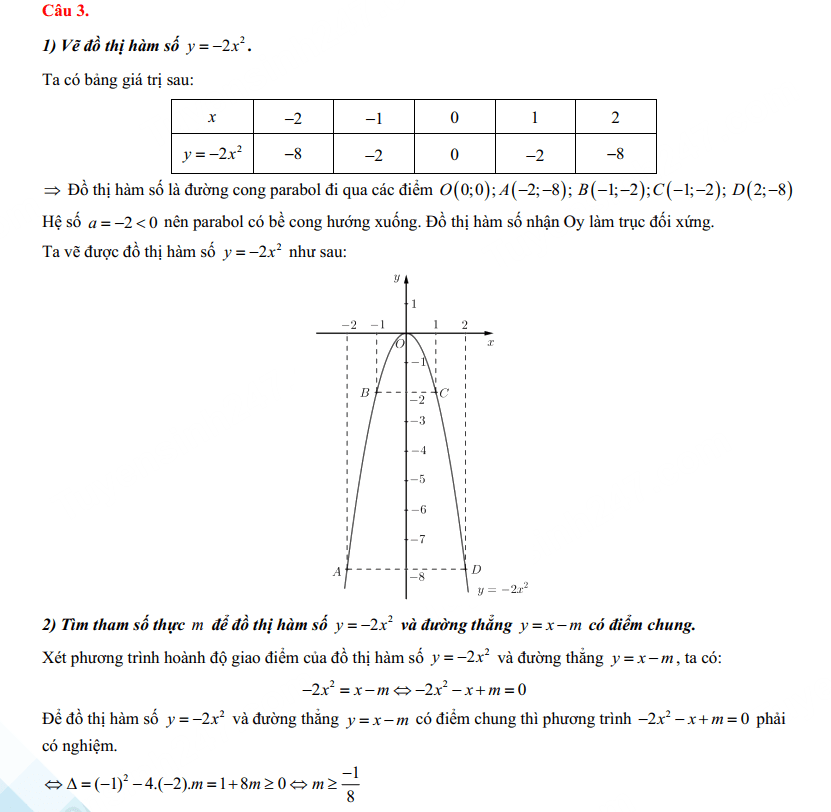
1. Vẽ đồ thị hàm số (P): y = x2
Parabol (P): y = x2 có bề lõm hướng lên và nhận Oy làm trục đối xứng
Ta có bảng giá trị sau:
x-2-1012y = x241014
⇒ Parabol (P): y = x2 đi qua các điểm (-2;4), (-1,1); (0;0), (1;1), (2,4)
Đồ thị Parabol (P): y = x2:
2) Tìm giá trị của tham số thực m để Parabol (P): y = x2 và đường thẳng có đúng một điểm chung.
Xét phương trình hoành độ giao điểm của (P), (d) ta được:
Để (P) cắt (d) có đúng một điểm chung khi và chi khi (1) có nghiệm kép
Vậy thỏa mãn yêu cầu bài toán.
3) Cho phương trình . Gọi là hai nghiệm phân biệt của phương trình, hãy tinh giả trị của biểu thức
Vì là hai nghiệm phân biệt của phương trình đã cho nên áp dụng hệ thức Vi-et với phương trình ta có: .
Ta có:
Vậy Q=9.
Câu 3: (1 điểm)
với 0, x neq 4right)” width=”112″ height=”22″ data-latex=”(left.x>0, x neq 4right)” data-i=”27″ class=”lazy” data-src=”https://tex.vdoc.vn/?tex=(%5Cleft.x%3E0%2C%20x%20%5Cneq%204%5Cright)”>
Với 0, x neq 4″ width=”98″ height=”20″ data-latex=”x>0, x neq 4″ data-i=”28″ class=”lazy” data-src=”https://tex.vdoc.vn/?tex=x%3E0%2C%20x%20%5Cneq%204″> ta có:
Vậy với 0, x neq 4″ width=”98″ height=”20″ data-latex=”x>0, x neq 4″ data-i=”33″ class=”lazy” data-src=”https://tex.vdoc.vn/?tex=x%3E0%2C%20x%20%5Cneq%204″> thì A=2.
Câu 4:
Câu 5
Mời các bạn tham khảo thêm các thông tin hữu ích khác trên chuyên mục Tài liệu của HoaTieu.vn.
Chào mừng bạn đến với PRAIM, - nền tảng thông tin, hướng dẫn và kiến thức toàn diện hàng đầu! Chúng tôi cam kết mang đến cho bạn một trải nghiệm sâu sắc và tuyệt vời về kiến thức và cuộc sống. Với Praim, bạn sẽ luôn được cập nhật với những xu hướng, tin tức và kiến thức mới nhất.
