Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 2 môn Toán lớp 10 sách Kết nối tri thức năm 2023 – 2024. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 2 Toán 10. Mời các bạn cùng đón xem:
Chỉ từ 100k mua trọn bộ Đề thi giữa học kì 2 Toán 10 Kết nối tri thức bản word có lời giải chi tiết (chỉ 20k cho 1 đề thi bất kì):
B1: Gửi phí vào tài khoản 0711000255837 – NGUYEN THANH TUYEN – Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official – nhấn vào đây
Xem thử tài liệu tại đây: Link tài liệu
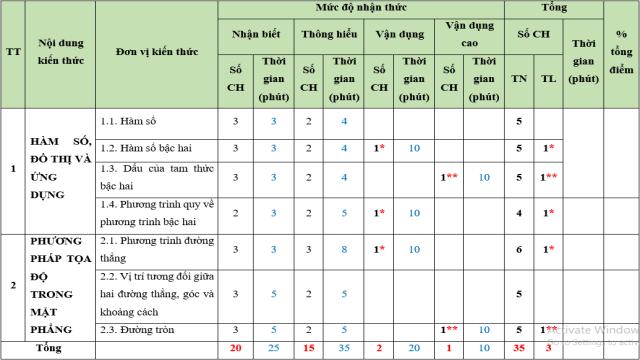
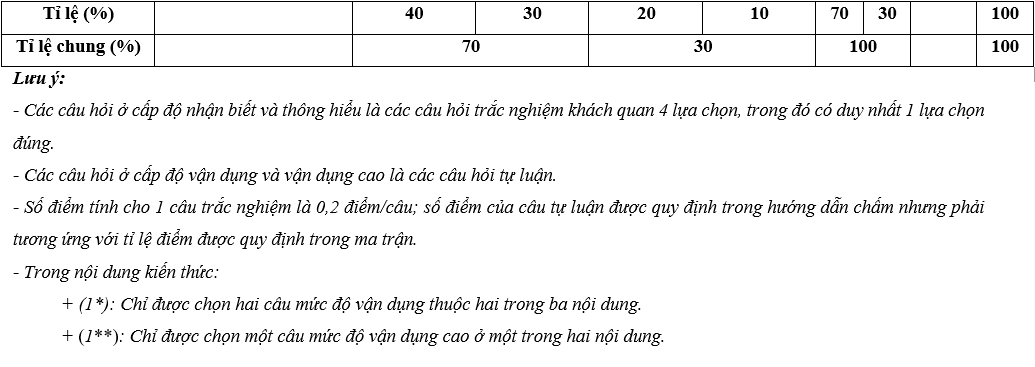
A. Ma trận đề thi giữa học kì 2
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
Câu hỏi trắc nghiệm: 35 câu (70%)
Câu hỏi tự luận : 3 câu (30%)
Đề thi giữa kì 2 Toán lớp 10 Kết nối tri thức có đáp án năm 2023 – 2024 – Đề 1
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 2 – Kết nối tri thức
Năm học 2023 – 2024
Môn: Toán 10
Thời gian làm bài: 90 phút
(Đề số 1)
I. Trắc nghiệm (7 điểm)
Câu 1. Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x?
A. x + 3y = 7;
B. x2 + y2 = 5;
C. y=x2−2;
D. y=2x.
Câu 2. Cho hàm số dưới dạng bảng như sau:
x
1
2
3
4
5
y
1
3
5
7
9
Giá trị của hàm số y tại x = 3 là
A. 2;
B. 3;
C. 5;
D. 7.
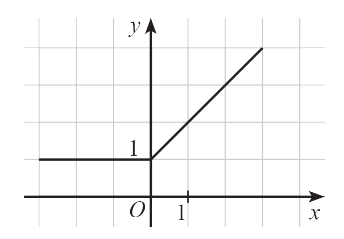
Câu 3. Cho hàm số y = f(x) có đồ thị như hình dưới.
Hàm số trên đồng biến trên khoảng
A. (0; 1);
B. (1; + ∞);
C. (0; + ∞);
D. (- ∞; 0).
Câu 4. Hàm số y=x+2×2−3x+2 có tập xác định là
A. (1; 2);
B. [1; 2];
C. {1; 2};
D. ℝ {1; 2}.
Câu 5. Cho hàm số y=2×2−5x. Giá trị của hàm số tại x = 10 là
A. 20;
B. 102;
C. 210;
D. Không tồn tại.
Câu 6. Trong các hàm số sau, hàm số nào không phải là hàm số bậc hai?
A. y = x2 – 5x + 3;
B. y = 1 – 2×2 + 4x;
C. y = x(x2 + x + 1);
D. y = 7 – x2.
Câu 7. Cho hàm số bậc hai y = 2×2 + 3x – 8. Hoành độ đỉnh của đồ thị hàm số bậc hai này là
A. −34;
B. 34;
C. 32;
D. −32.
Câu 8. Hàm số bậc hai y = 2 – 3×2 + 4x có hệ số tự do là
A. 2;
B. – 3;
C. 4;
D. – 2.
Câu 9. Cho hàm số bậc hai f(x) = 2×2 – 8x + 7. Phát biểu nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (- ∞; 2), nghịch biến trên khoảng (2; + ∞);
B. Hàm số đồng biến trên khoảng (- ∞; 4), nghịch biến trên khoảng (4; + ∞);
C. Hàm số đồng biến trên khoảng (4; + ∞), nghịch biến trên khoảng (- ∞; 4);
D. Hàm số đồng biến trên khoảng (2; + ∞), nghịch biến trên khoảng (- ∞; 2).
Câu 10. Xác định parabol y = ax2 + c, biết rằng parabol này đi qua hai điểm A(1; 1) và B(2; – 2).
A. y = – x2 + 2;
B. y = x2 + 2;
C. y = 2×2 – 1;
D. y = 2×2 + 1.
Câu 11. Tìm khẳng định đúng trong các khẳng định sau.
A. f(x) = 3×2 + x – 4 là tam thức bậc hai;
B. f(x) = 3x – 5 là tam thức bậc hai;
C. f(x) = 2×3 + 3x – 2 là tam thức bậc hai;
D. f(x) = (x2)2 – x2 + 3 là tam thức bậc hai.
Câu 12. Cho hàm số f(x) = ax2 + bx + c, (a ≠ 0) và ∆ = b2 – 4ac. Cho biết dấu của ∆ khi f(x) luôn cùng dấu với hệ số a với mọi x ∈ ℝ.
A. ∆ ≤ 0;
B. ∆ = 0;
C. ∆ > 0;
D. ∆ < 0.
Câu 13. Cho tam thức f(x) = x2 – 8x + 16. Khẳng định nào sau đây là đúng?
A. Phương trình f(x) = 0 vô nghiệm;
B. f(x) > 0 với mọi x ∈ ℝ;
C. f(x) ≥ 0 với mọi x ∈ ℝ;
D. f(x) < 0 khi x < 4.
Câu 14. Trong các phát biểu sau, phát biểu nào sai?
A. x2 – 3x + 2 > 0 khi x ∈ (- ∞; 1) ∪ (2; + ∞);
B. x2 – 3x + 2 ≤ 0 khi x ∈ [1; 2];
C. x2 – 3x + 2 < 0 khi x ∈ [1; 2);
D. x2 – 3x + 2 ≥ 0 khi x ∈ (- ∞; 1] ∪ [2; + ∞).
Câu 15. Tập nghiệm của bất phương trình x2 – 7x + 10 < 0 là
A. S = (- ∞; 2] ∪ [5; + ∞);
B. S = (- ∞; 2) ∪ (5; + ∞);
C. S = [2; 5];
D. S = (2; 5).
Câu 16. Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình ax2+bx+c=dx+e là tập nghiệm của phương trình ax2 + bx + c = (dx + e)2;
B. Tập nghiệm của phương trình ax2+bx+c=dx+e là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình dx + e ≥ 0;
C. Mọi nghiệm của phương trình ax2 + bx + c = (dx + e)2 đều là nghiệm của phương trình ax2+bx+c=dx+e;
D. Tập nghiệm của phương trình ax2+bx+c=dx+e là tập hợp các nghiệm của phương trình ax2 + bx + c = (dx + e)2 thỏa mãn bất phương trình ax2 + bx + c ≥ 0.
Câu 17. Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình ax2+bx+c=dx2+ex+f là tập nghiệm của phương trình ax2 + bx + c = dx2 + ex + f;
B. Tập nghiệm của phương trình ax2+bx+c=dx2+ex+f là tập nghiệm của phương trình (ax2 + bx + c)2 = (dx2 + ex + f)2;
C. Mọi nghiệm của phương trình ax2 + bx + c = dx2 + ex + f đều là nghiệm của phương trình ax2+bx+c=dx2+ex+f;
D. Tập nghiệm của phương trình ax2+bx+c=dx2+ex+f là tập hợp các nghiệm của phương trình ax2 + bx + c = dx2 + ex + f thỏa mãn bất phương trình ax2 + bx + c ≥ 0 (hoặc dx2 + ex + f ≥ 0).
Câu 18. Số nghiệm của phương trình 4−3×2=2x−1 là
A. 0;
B. 1;
C. 2;
D. 3.
Câu 19. Giá trị nào sau đây là một nghiệm của phương trình3x2−6x+1=x2−3?
A. 2;
B. 4;
C. 12;
D. 20.
Câu 20. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 3 = 0. Vectơ pháp tuyến của đường thẳng d là
A. n→=1; −2;
B. n→=1; 2;
C. n→=2; −1;
D. n→=2; 1.
Câu 21. Điểm nào dưới đây thuộc đường thẳng d: 3x – 2y + 4 = 0?
A. A(1; 2);
B. B(0; 2);
C. C(2; 0);
D. D(2; 1).
Câu 22. Phương trình tham số của đường thẳng ∆ đi qua điểm A(3; 1) và nhận u→=3; −1 làm vectơ chỉ phương là
A. x=3+3ty=1−t;
B. x=3+3ty=1+t;
C. x=3+3ty=−1+t;
D. x=3+3ty=−1−t.
Câu 23. Phương trình tổng quát của đường thẳng d đi qua điểm A(2; – 2) và nhận n→=1; 3 làm vectơ pháp tuyến là
A. x – y + 2 = 0;
B. – 3x + y + 4 = 0;
C. x – 3y + 4 = 0;
D. x + 3y + 4 = 0.
Câu 24. Cho đường thẳng d có phương trình tham số x=5+ty=−9−2t. Phương trình tổng quát của đường thẳng d là
A. 2x + y – 1 = 0;
B. – 2x + y – 1 = 0;
C. x + 2y + 1 = 0;
D. 2x + 3y – 1 = 0.
Câu 25. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(- 2; 3) và B(4; – 1). Phương trình nào sau đây là phương trình đường thẳng AB?
A. x + y – 3 = 0;
B. y = 2x + 2;
C. x−46=y−1−4;
D. x=1+3ty=1−2t.
Câu 26. Trong mặt phẳng tọa độ, xét hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0.
và hệ phương trình: a1x+b1y+c1=0a2x+b2y+c2=0 (*).
Khi đó, ∆1 song song với ∆2 khi và chỉ khi
A. hệ (*) có vô số nghiệm;
B. hệ (*) vô nghiệm;
C. hệ (*) có nghiệm duy nhất;
D. hệ (*) có hai nghiệm.
Câu 27. Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0. Khoảng cách từ điểm M đến đường thẳng ∆, kí hiệu là d(M, ∆), được tính bởi công thức
A. dM, Δ=ax0+by0+ca2+b2;
B. dM, Δ=ax0+by0+ca2+b2;
C. dM, Δ=ax0+by0+cx02+y02;
D. dM, Δ=ax0+by0+cx02+y02.
Câu 29. Khoảng cách từ điểm A(1; 1) đến đường thẳng d: 5x – 12y – 6 = 0 là
A. 13;
B. – 13;
C. – 1;
D. 1.
Câu 30. Góc giữa hai đường thẳng a: 3x – y + 7 = 0 và b: x – 3y – 2 = 0 là
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Câu 31. Phương trình nào sau đây là phương trình đường tròn?
A. 2×2 + y2 – 6x – 6y – 8 = 0;
B. x2 + 2y2 – 4x – 8y – 12 = 0;
C. x2 + y2 – 2x – 8y + 18 = 0;
D. 2×2 + 2y2 – 4x + 6y – 12 = 0.
Câu 32. Đường tròn (x + 1)2 + (y – 2)2 = 16 có bán kính bằng bao nhiêu?
A. 16;
B. 4;
C. 256;
D. 8.
Câu 33. Phương trình nào sau đây là phương trình của đường tròn tâm I(- 1; 2), có bán kính bằng 5?
A. (x – 1)2 + (y + 2)2 = 25;
B. (x + 1)2 + (y + 2)2 = 25;
C. (x + 1)2 + (y – 2)2 = 25;
D. (x – 1)2 + (y – 2)2 = 25.
Câu 34. Phương trình đường tròn có tâm I(3; 4) tiếp xúc với đường thẳng ∆: 3x + 4y – 10 = 0 là
A. (x – 3)2 + (y – 4)2 = 9;
B. (x + 3)2 + (y – 4)2 = 9;
C. (x – 3)2 + (y – 4)2 = 3;
D. (x + 3)2 + (y + 4)2 = 3.
Câu 35. Trong mặt phẳng tọa độ, cho đường tròn (C): (x – 2)2 + (y + 2)2 = 5. Tiếp tuyến tại điểm M(1; 0) thuộc đường tròn (C) có phương trình là
A. y = – 2;
B. x = 1;
C. x + 2y – 1 = 0;
D. x – 2y – 1 = 0.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Giả sử độ cao h (đơn vị: mét) của một quả bóng golf tính theo thời gian t (đơn vị: giây) trong một lần đánh của vận động viên được xác định bằng một hàm số bậc hai và giá trị tương ứng tại một số thời điểm được cho bởi bảng dưới đây:
Thời gian (s)
0,5
1
2
3
Độ cao (m)
28
48
64
48
a) Xác định hàm số bậc hai biểu thị độ cao h(m) của quả bóng gofl tính theo thời gian t(s).
b) Sau bao lâu kể từ khi vận động viên đánh bóng thì bóng lại chạm đất?
Bài 2. (1 điểm) Cho đường thẳng d1: 2x – y – 2 = 0; d2: x + y + 3 = 0 và điểm M(3; 0). Viết phương trình đường thẳng ∆ đi qua điểm M, cắt d1 và d2 lần lượt tại A và B sao cho M là trung điểm của đoạn AB.
Bài 3. (1 điểm) Cho đường tròn (C): (x – 1)2 + (y – 2)2 = 4 và đường thẳng d: x – y – 1 = 0. Viết phương trình đường tròn (C’) đối xứng của (C) qua d. Tìm tọa độ giao điểm của (C), (C’).
Chào mừng bạn đến với PRAIM, - nền tảng thông tin, hướng dẫn và kiến thức toàn diện hàng đầu! Chúng tôi cam kết mang đến cho bạn một trải nghiệm sâu sắc và tuyệt vời về kiến thức và cuộc sống. Với Praim, bạn sẽ luôn được cập nhật với những xu hướng, tin tức và kiến thức mới nhất.
- Hướng dẫn cách cài đặt và chơi game Android trên máy tính chạy Windows
- Bộ Sưu Tập hình nền chúa Full HD Cực Độc
- Top 9 nguồn truyện tranh tiếng Anh free nạp từ vựng hiệu quả
- Cách làm ếch xào sả ớt ngon cay đậm đà, đưa cơm
- Lời Chúc Chia Tay Giáo Viên Về Hưu – Hãy để hành trình mới tràn đầy niềm vui và hạnh phúc!