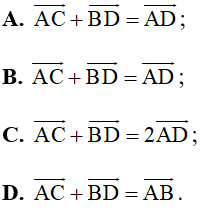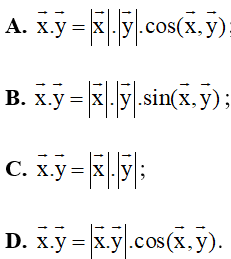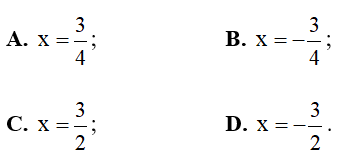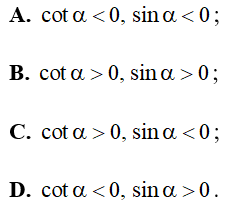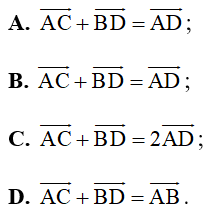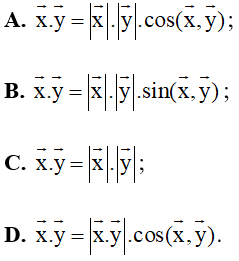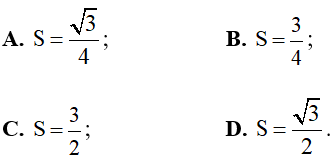TOP 10 đề thi Học kì 1 Toán lớp 10 (Cánh diều) 2023 có đáp án

Chỉ 150k mua trọn bộ Đề thi Toán 10 Cánh diều bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 – NGUYEN THANH TUYEN – Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official – nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Học kì 1 Toán lớp 10 (Cánh diều) 2023 có đáp án

MA TRẬN ĐỀ THI HỌC KỲ 1 TOÁN LỚP 10 – ĐỀ SỐ 1

TT

Nội dung/bài/chủ đề

Mức độ

Số câu

Ghi chú

Nhận biết

Thông hiểu

Vận dụng

Vận dụng cao

TN

TL

1

Mệnh đề toán học

1

1

2

0,4 điểm

2

Tập hợp và các phép toán trên tập hợp

1

1

2

0,4 điểm

3

Hệ bất phương trình bậc nhất hai ẩn

1

1

0,2 điểm

4

Hàm số, hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

1

3

1

5

1,0 điểm

5

Dấu của tam thức bậc hai. Bất phương trình bậc hai một ẩn

1

1

1

2

1

2,4 điểm

6

Hai dạng phương trình quy về dạng phương trình bậc hai

1

1

2

0,4 điểm

7

Định lí cosin và định lí sin. Giải tam giác

1

1

0,2 điểm

8

Khái niệm vectơ

2

2

0,4 điểm

9

Tổng, hiệu của các vectơ.

1

2

1

3

1

1,6 điểm

10

Tích của một vectơ với một số.

2

1

1

3

1

1,6 điểm

11

Tích vô hướng của hai vectơ

1

1

1

1

2

2

1,4 điểm

Tổng số

8

12

7

3

0,2×25

= 5 điểm

5 điểm

10 điểm

Phòng Giáo dục và Đào tạo …..

Đề khảo sát chất lượng Học kì 1

Năm học …

Môn: Toán 10

Thời gian làm bài: ………..

Đề thi Học kì 1 Toán lớp 10 Cánh diều có đáp án – Đề số 1

A. TRẮC NGHIỆM (5,0 điểm)

Câu 1. Trục đối xứng của parabol y = x2 + 3x – 1 là đường thẳng:

A. x=34;

B. x=−34;

C. x=32;

D. x=−32.

Câu 2. Cho α là góc nhọn. Khẳng định nào sau đây đúng?

A. cotα<0,  sinα<0;

B. cotα>0,  sinα>0;

C. cotα>0,  sinα<0;

D. cotα<0,  sinα>0.

Câu 3. Cho hình bình hành ABCD. Khẳng định nào sau đây đúng?

Câu 4. Cho tam giác ABC vuông tại A, AB = 2, ABC^=72°. Độ dài của vectơ BA→+AC→ gần với giá trị nào nhất sau đây:

A. 2,1;

B. 6,5;

C. 2,5;

D. 6,0.

Câu 5. Mệnh đề phủ định của mệnh đề “∃x ∈ ℝ, x3 – 2x + 1 < 0” là:

A. ∀x ∈ ℝ, x3 – 2x + 1 ≥ 0;

B. ∀x ∈ ℝ, x3 – 2x + 1 < 0”;

C. ∃x ∈ ℝ, x3 – 2x + 1 ≥ 0”;

D. ∀x ∈ ℝ, x3 – 2x + 1 > 0”.

Câu 6. Cho hai vectơ x→,  y→ đều khác vectơ 0→> Tích vô hướng của x→ và y→ được xác định bởi công thức

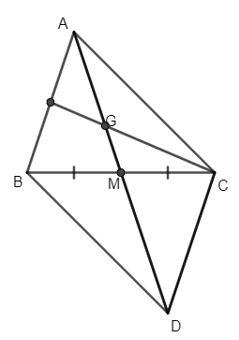
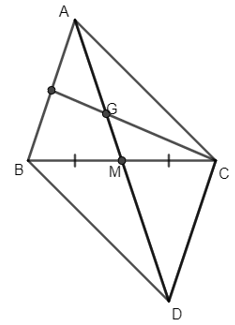
Câu 7. Cho hình bình hành ABCD, có M là trung điểm của BC, G là trọng tâm của tam giác ABC (tham khảo hình vẽ bên). Khi đó AD→=kAG→. Vậy k bằng:

A. k=23;

B. k=13;

C. k=32;

D. k = 3.

Câu 8. Cho hai tập hợp A = {- 3; – 1; 1; 2; 4; 5} và B = {- 2; – 1; 0; 2; 3; 5}. Tập hợp AB:

A. A B = {- 3; 1; 4};

B. A B = { – 2; 0; 3};

C. A B = {- 1; 2; 5};

D. AB=−3;−1;2;5.

Câu 9. Tập hợp A = {x ∈ ℝ| – 2 ≤ x < 0} viết lại dưới dạng khác là:

A. A = (- 2; 0];

B. A = [- 2; 0];

C. A = [- 2; 0);

D. A = {- 2; – 1}.

Câu 10. Khẳng định nào sau đây đúng?

A. Đồ thị của một hàm số chẵn nhận trục hoành làm trục đối xứng.

B. Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.

C. Đồ thị của một hàm số chẵn nhận gốc tọa độ làm tâm đối xứng.

D. Đồ thị của một số chẵn đi qua gốc tọa độ.

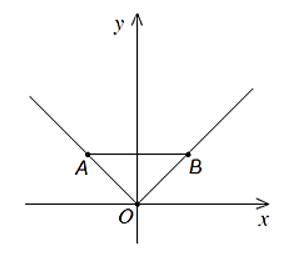
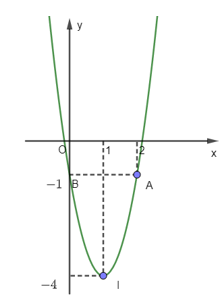
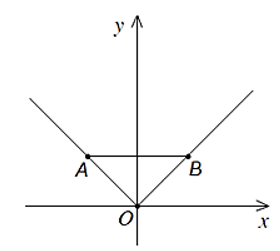
Câu 11. Hai điểm A, B nằm trên đồ thị hàm số y = |x| và đối xứng với nhau qua trục tung. Biết AB=3>, diện tích S của tam giác OAB là (biết O là gốc tọa độ, tham khảo đồ thị hàm số y = |x| ở hình vẽ bên).

A. S=34;

B. S=34;

C. S=32;

D. S=32.

Câu 12. Cho a→=(2 ; −1),  b→=(4 ; −2). Tọa độ của vectơ 12a→−34 b→ là:

A. (1; – 1);

B. (- 2; 1);

C. (4; – 2);

D. (- 3; 5).

Câu 13. Cho hình vuông ABCD. Có bao nhiêu vectơ cùng phương với vectơ AB→:

A. 1;

B. 2;

C. 3;

D. 0.

Câu 14. Giá trị nào dưới đây là nghiệm của phương trình x+1−x2=−1?

A. x = 0;

B. x = – 1;

C. x = 0 và x = – 1;

D. Không tồn tại x là nghiệm của phương trình.

Câu 15. Cho tam giác ABC vuông tại A, AB = 2, AC = 5, ABC^=34°.Tính CA→.BC→:

A. 7,4;

B. – 7,4;

C. 4,4;

D. – 4,4.

Câu 16. Cho parabol (P):

Hình vẽ trên là đồ thị của hàm số bậc hai nào dưới đây:

A. y = 3×2 – 6x – 1;

B. y = x2 – 2x – 1;

C. y = – x2 + 2x + 1;

D. y = – 3×2 + 6x – 1.

Câu 17. Hàm số nào sau đây là hàm số lẻ?

A. f(x) = x3 + 1;

B. f(x) = 2×4 + 3;

C. f(x) = |x|;

D. f(x) = x3.

Câu 18. Trong các phát biểu sau, phát biểu nào đúng?

A. Tập nghiệm phương trình f(x)=g(x) là tập nghiệm của phương trình f(x) = g(x);

B. Tập nghiệm phương trình f(x)=g(x) là tập nghiệm của phương trình [f(x)]2 = [g(x)]2;

C. Mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình f(x)=g(x);

D. Tập nghiệm của phương trình f(x)=g(x) là tập hợp các nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).

Câu 19. Cho tứ giác ABCD. Xác định điểm M thỏa mãn: 3MA→+MB→+MC→+MD→=0→

A. M là điểm thỏa mãn MA = MG;

B. M là trung điểm của AG;

C. M thuộc đoạn AG thỏa mãn MA = 3 MG;

D. M thuộc trung trực của đoạn thẳng AG.

Câu 20. Cho tứ giác ABC có AB = 5, AC = 4, BAC^=92°. Khi đó độ dài BC khoảng:

A. 42,4;

B. 6,5;

C. 3;

D. 3,2.

Câu 21. Gọi S là tập nghiệm của bất phương trình – x2 + 2x – 4 ≤ 0. Khi đó S bằng:

A. ℝ;

B. ℝ{2; 4};

C. ∅;

D. {2; 4}.

Câu 22. Cho hệ bất phương trình x+y≥−4x−3y<0x>0. Điểm nào thuộc miền nghiệm của hệ bất phương trình đã cho?

A. M(- 5; 1);

B. N(4; 1);

C. P(0; 1);

D. Q(1; 2).

Câu 23. Với giá trị nào của tham số m thì tam thức f(x) = – x2 – 3x + m – 5 không dương với mọi x:

A. m = 2;

B. m = 4;

C. m = 3;

D. m = 6.

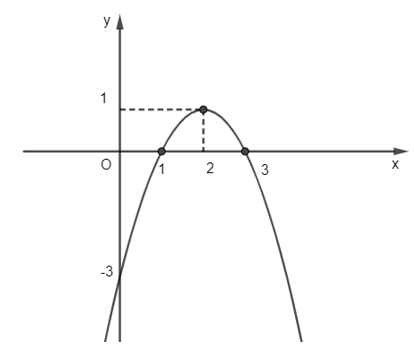
Câu 24. Dựa vào đồ thị hàm số bậc hai y = f(x) (như hình vẽ) hãy tìm tập nghiệm của bất phương trình f(x) > 0:

A. [1; 3];

B. (1; 3];

C. (1; 3);

D. {1; 2; 3}.

Câu 25. Nếu hai điểm M và N thỏa mãn: MN→.NM→=−16 thì độ dài đoạn MN bằng:

A. 8;

B. 4;

C. 2;

D. 64.

B. TỰ LUẬN (3,0 điểm)

Bài 1. (1,0 điểm)

a) Lập bảng biến thiên và vẽ đồ thị của hàm số y = x2 – 5x.

b) Tìm các giá trị của tham số m để phương trình x2−(2m−1)x−m2+5m−1=x+1 có một nghiệm duy nhất.

Bài 2. (1,0 điểm)

a) Trong mặt phẳng tọa độ Oxy cho hai vectơ a→ và b→ có a→=2,5, b→=4,6 và a→.b→=−5,75. Tính cos(a→,b→).

b) Cho tam giác ABC , M là trung điểm của cạnh BC điểm N nằm trên cạnh AC sao cho NA = 2NC , D là trung điểm của AN. Chứng minh AC→+3DA→=0→ và AC→−3AB→=6MN→.

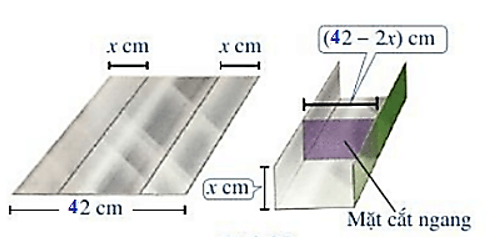
Bài 3. (1,0 điểm) Bác Nam muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 40 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông sao cho độ cao hai thành rãnh bằng nhau. Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 160 cm2. Bác Nam cần làm rãnh nước có độ cao ít nhất là bao nhiêu xăng – ti – mét để đảm bảo kĩ thuật?

Đáp án đề thi Học kì 1 Toán lớp 10 Cánh diều – Đề số 1

A. TRẮC NGHIỆM (7,0 điểm)

Câu 1

D

Câu 6

A

Câu 11

B

Câu 16

A

Câu 21

B

Câu 2

B

Câu 7

D

Câu 12

B

Câu 17

D

Câu 22

D

Câu 3

C

Câu 8

A

Câu 13

C

Câu 18

D

Câu 23

C

Câu 4

B

Câu 9

C

Câu 14

B

Câu 19

B

Câu 24

C

Câu 5

A

Câu 10

B

Câu 15

B

Câu 20

B

Câu 25

B

Hướng dẫn đáp án chi tiết

Câu 1. Trục đối xứng của parabol y = x2 + 3x – 1 là đường thẳng:

Đáp án đúng là D

Parabol y = x2 + 3x – 1 có trục đối xứng là đường thẳng x=−32.

Câu 2. Cho α là góc nhọn. Khẳng định nào sau đây đúng?

Đáp án đúng là B

Vì α là góc nhọn nên sinα > 0 và cosα > 0

⇒ cotα = cosαsinα>0

Vậy chọn đáp án B.

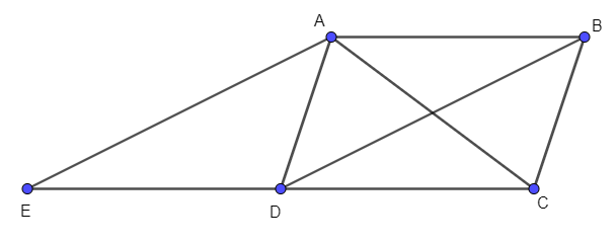
Câu 3. Cho hình bình hành ABCD. Khẳng định nào sau đây đúng?

Đáp án đúng là C

Lấy điểm E sao cho ABDE là hình bình hành, khi đó AE→=BD→, AB→=ED→

Suy ra AB = ED mà AB = CD nên DE = DC hay D là trung điểm của EC.

Ta có: AC→+BD→=AC→+AE→=2AD→ (quy tắc hình bình hành).

Câu 4. Cho tam giác ABC vuông tại A, AB = 2, ABC^=72°. Độ dài của vectơ BA→+AC→ gần với giá trị nào nhất sau đây:

A. 2,1;

B. 6,5;

C. 2,5;

D. 6,0.

Đáp án đúng là B

Ta có: BA→+AC→=BC→

⇒ BA→+AC→=BC→=BC

Xét tam giác ABC vuông tại A có:

cosB = ABBC

⇔ cos72° = 2BC

⇔ BC = 2BC.

Vậy độ dài của vectơ BA→+AC→ gần vớ 6,5.

Câu 5. Mệnh đề phủ định của mệnh đề “∃x ∈ ℝ, x3 – 2x + 1 < 0” là:

A. ∀x ∈ ℝ, x3 – 2x + 1 ≥ 0;

B. ∀x ∈ ℝ, x3 – 2x + 1 < 0”;

C. ∃x ∈ ℝ, x3 – 2x + 1 ≥ 0”;

D. ∀x ∈ ℝ, x3 – 2x + 1 > 0”.

Đáp án đúng là A

Mệnh đề phủ định của mệnh đề “∃x ∈ ℝ, x3 – 2x + 1 < 0” là ∀x ∈ ℝ, x3 – 2x + 1 ≥ 0.

Câu 6. Cho hai vectơ x→,  y→ đều khác vectơ 0→. Tích vô hướng của x→ và y→ được xác định bởi công thức

Đáp án đúng là A

Tích vô hướng của x→ và y→ được xác định bởi công thức x→.y→=x→.y→.cos(x→,y→) .

Câu 7. Cho hình bình hành ABCD, có M là trung điểm của BC, G là trọng tâm của tam giác ABC (tham khảo hình vẽ bên). Khi đóAD→=kAG→. Vậy k bằng:

A. k=23;

B. k=13;

C. k=32;

D. k = 3.

Đáp án đúng là D

Vì G là trọng tâm tam giác ABC nên ta có: AG→=23AM→.

Mặt khác ABCD là hình bình hành, M là trung điểm của BC nên AM→=12AD→

⇒ AG→=23AM→=23.12AD→=13AD→ hayAD→=3AG→.

Vậy k = 3.

Câu 8. Cho hai tập hợp A = {- 3; – 1; 1; 2; 4; 5} và B = {- 2; – 1; 0; 2; 3; 5}. Tập hợp AB:

A. A B = {- 3; 1; 4};

B. A B = { – 2; 0; 3};

C. A B = {- 1; 2; 5};

D. A B = {-3;-1; 2; 5}.

Đáp án đúng là A

Ta có tập hợp A B là tập hợp các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B nên khi đó ta có: A B = {- 3; 1; 4}.

Câu 9. Tập hợp A = {x ∈ ℝ| – 2 ≤ x < 0} viết lại dưới dạng khác là:

A. A = (- 2; 0];

B. A = [- 2; 0];

C. A = [- 2; 0);

D. A = {- 2; – 1}.

Đáp án đúng là C

Ta có: A = {x ∈ ℝ| – 2 ≤ x < 0} = [- 2; 0).

Câu 10. Khẳng định nào sau đây đúng?

A. Đồ thị của một hàm số chẵn nhận trục hoành làm trục đối xứng.

B. Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.

C. Đồ thị của một hàm số chẵn nhận gốc tọa độ làm tâm đối xứng.

D. Đồ thị của một số chẵn đi qua gốc tọa độ.

Đáp án đúng là B

Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.

Câu 11. Hai điểm A, B nằm trên đồ thị hàm số y = |x| và đối xứng với nhau qua trục tung. BiếtAB=3, diện tích S của tam giác OAB là (biết O là gốc tọa độ, tham khảo đồ thị hàm số y = |x| ở hình vẽ bên).

Đáp án đúng là B

Vì A và B đối xứng với nhau qua Oy nên AB ⊥ Oy

Mà Ox ⊥ Oy nên AB // Ox

Kẻ AH vuông góc với Ox và gọi K là trung điểm của AB.

Ta có AB=3 nên AK = KB = 32 hay OH = 32. Suy ra xA = 32.

Mặt khác A thuộc vào đồ thị hàm số nên yA = |xA| = 32.

⇒ OK = 32

Diện tích tam giác OAB là: SOAB = 12.OK.AB=12.32.3=34 (đvdt).

Vậy diện tích tam giác OAB là S=34.

Câu 12. Cho a→=(2 ; −1),  b→=(4 ; −2). Tọa độ của vectơ 12a→−34 b→ là:

A. (1; – 1);

B. (- 2; 1);

C. (4; – 2);

D. (- 3; 5).

Đáp án đúng là B

Ta có:

12a→=12(2 ; −1)=1;−12;

34b→=34(4 ; −2)=3;−32.

Khi đó: 12a→−34b→=1−3;−12+32=−2;1.

Câu 13. Cho hình vuông ABCD. Có bao nhiêu vectơ cùng phương với vectơ AB→:

A. 1;

B. 2;

C. 3;