Câu 1: Cho $int_{0}^{1}f(x)dx$ = 1 và $int_{1}^{2}f(2x-1)dx$ = 6. Tính tích phân $int_{0}^{3}f(x)dx$ bằng:
- A. 7
- B. 5
-
C. 13
- D. 4
Câu 2: Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ dưới đây:
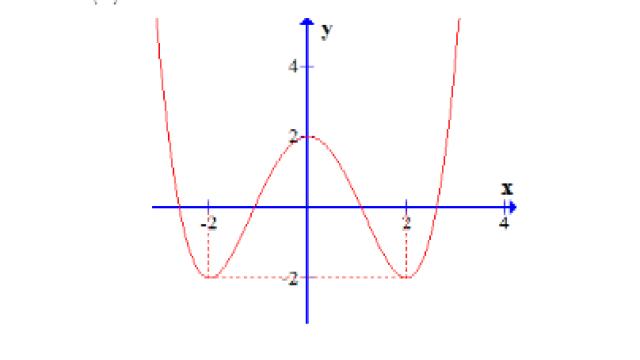
Số nghiệm thực của phương trình 4|f(x)| – 5 = 0 là:
-
A. 8
- B. 4
- C. 7
- D. 6
Câu 3: Tính đạo hàm của hàm số y = $log_{2}$(3x+1):
- A. y’ = $frac{1}{(3x+1)ln2}$
- B. y’ = $frac{3}{3x+1}$
- C. y’ = $frac{1}{3x+1}$
-
D. y’ = $frac{3}{(3x+1)ln2}$
Câu 4: Tìm nghiệm của phương trình $log_{2}(1-x)$ = 2
-
A. x = -3
- B. x = -4
- C. x = 3
- D. x = 5
Câu 5: Gọi (H) là hình phẳng giới hạn bởi các đường y = x-2; y = 0; x = -3; x = 4. Thể tích của khối tròn xoay khi cho (H) quay quanh trục Ox bằng:
- A. $frac{21pi }{2}$
- B. $frac{29pi }{2}$
-
C. $frac{133pi }{3}$
- D. 7$pi $
Câu 6: Cho phương trình $5^{x}+m=log_{5}(x-m)$ với m là tham số. Có bao nhiêu giá trị nguyên của m $in $ (-20;20) để phương trình đã cho có nghiệm?
- A. 20
-
B. 19
- C. 9
- D. 21
Câu 7: Số phức có phần thực bằng 3 và phần ảo bằng -4 là:
- A. 3+4i
-
B. 3-4i
- C. 4-3i
- D. 4+3i
Câu 8: Cho hàm số y = $ax^{4}+bx^{2}+c$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

- A. a>0, b<0, c<0
- B. a<0, b<0, c<0
-
C. a<0, b>0, c<0
- D. a>0, b<0, c>0
Câu 9: Cho hàm số f(x) liên tục trên R. Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x), y=0, x=-1, x=2 (như hình vẽ). Mệnh để nào dưới đây đúng?
-
A. S = $int_{-1}^{1}f(x)dx – int_{1}^{2}f(x)dx$
- B. S = $int_{-1}^{1}f(x)dx + int_{1}^{2}f(x)dx$
- C. S = $int_{-1}^{2}f(x)dx$
- D. S = -$int_{-1}^{2}f(x)dx$
Câu 10: Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình vẽ.

Hàm số y = f($x^{2}$) nghịch biến trên khoảng:
-
A. (-1;10)
- B. (-2;-1)
- C. (1;4)
- D. (0;1)
Câu 11: Trong không gian Oxyz, cho mặt cầu (S): $x^{2}+y^{2}+z^{2}-2x-4y-4z-16=0$. Bán kính của mặt cầu (S) là:
-
A. 5
- B. 4
- C. $2sqrt{5}$
- D. $sqrt{52}$
Câu 12: Cho khối chóp S.ABCD có thể tích bằng $2a^{3}$, đáy ABCD là hình thang với đáy lớn là AB và AB = 3CD. Gọi M là trung điểm cạnh SA, N là điểm thuộc cạnh CB sao cho BN = 3NC. Mặt phẳng (DMN) cắt cạnh SB tại I. Tính thể tích khối chóp AMDNI.
- A. $frac{3a^{3}}{8}$
- B. $frac{5a^{3}}{8}$
- C. $frac{10a^{3}}{12}$
-
D. $frac{3a^{3}}{4}$
Câu 13: Cho ba số dương a, b, c ($aneq 1; bneq 1$) và số thực $alpha neq 0$. Đẳng thức nào sau đây là sai?
-
A. $log_{b}c = frac{log_{a}c}{log_{a}b}$
- B. $log_{a}bc = log_{a}b+log_{a}c$
- C. $log_{a}frac{b}{c} = log_{a}b-log_{a}c$
- D. $log_{a}b^{alpha }=frac{1}{alpha }log_{a}b$
Câu 14: Đồ thị hàm số y = $frac{x-3}{x^{2}-9}$ có mấy đường tiệm cận:
- A. 0
- B. 3
- C. 1
-
D. 2
Câu 15: Cho hàm số y = $x^{3}-3x^{2}+x$ có đồ thị (C). Phương trình tiếp tuyến của (C) có hệ số góc nhỏ nhất là:
- A. y = -x
- B. y = -2x+3
-
C. y = -2x+1
- D. y = x
Câu 16: Số phức liên hợp của số phức z = -1+2i là:
- A. 2+i
- B. 1+2i
-
C. -1-2i
- D. 1-2i
Câu 17: Hàm số y = $frac{2x+3}{x+1}$ có bao nhiêu điểm cực trị?
- A. 3
- B. 1
- C. 2
-
D. 0
Câu 18: Tập nghiệm của bất phương trình $log_{frac{1}{2}}(2x-1)>-1$ là:
-
A. $(frac{1}{2};frac{3}{2})$
- B. $(frac{3}{2};+infty )$
- C. $(1;frac{3}{2})$
- D. $(-infty ;frac{3}{2})$
Câu 19: Trong không gian Oxyz, cho đường thẳng d: $frac{x-1}{2}=frac{y-2}{3}=frac{z+2}{-1}$. Điểm nào dưới đây thuộc đường thẳng d:
- A. (5;1;-4)
- B. (-1;-1;1)
-
C. (3;5;-3)
- D. (1;2;2)
Câu 20: Cho x, y thuộc R thỏa mãn x+3y+(2x-y)i=13+5i. Giá trị của biểu thức $x^{2}-y^{2}$ bằng:
- A. 10
-
B. 7
- C. 25
- D. 5
Câu 21: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 2x-3y+z+4=0. Vecto nào dưới đây là một vecto pháp tuyến của mặt phẳng (P):
- A. (-2;3;4)
- B. (2;-3;4)
- C. (2;-3;0)
-
D. (2;-3;1)
Câu 22: Rút gọn biểu thức P = $(5-2sqrt{6})^{2020}.(5+2sqrt{6})^{2020}$ được kết quả bằng:
- A. 1
- B. 2
- C. 49 + 20$sqrt{6}$
-
D. 49 – 20$sqrt{6}$
Câu 23: Thể tích của khối trụ có chiều cao bằng h và diện tích đáy bằng B là:
-
A. V = Bh
- B. V = $frac{1}{4}$Bh
- C. V = $frac{1}{3}$Bh
- D. V = $frac{1}{2}$Bh
Câu 24: Cho hình chóp S.ABC. Gọi M, N, P lần lượt là trung điểm của SA, SB, SC. Tỉ số thể tích $frac{V_{S.ABC}}{V_{S.MNP}}$ bằng:
- A. 2
-
B. 8
- C. 12
- D. 3
Câu 25: Tích các nghiệm của phương trình $2^{2x^{2}-5x-1} = frac{1}{2}$ là:
- A. 2
-
B. 0
- C. -2
- D. $frac{5}{2}$
Câu 26: Cho hàm số f(x) có đạo hàm f'(x) = $x(x-1)^{2}(x+4)^{8}$ với mọi x thuộc R. Số điểm cực trị của hàm số đã cho là:
- A. 6
- B. 1
- C. 3
-
D. 2
Câu 27: Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB = a, AD = a$sqrt{3}$, SA vuông góc với mặt phẳng đáy và SC tạo với đáy một góc $60^{circ}$. Thể tích của khối chóp S.ABCD bằng:
-
A. 2$a^{3}$
- B. $a^{3}sqrt{3}$
- C. $frac{a^{3}sqrt{3}}{3}$
- D. 6$a^{3}$
Câu 28: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

- A. y = $x^{3}+3x+1$
- B. y = $frac{-1}{3}x^{3}+x+1$
- C. y = $x^{4}-2x^{2}+1$
-
D. y = $x^{3}-3x+1$
Câu 29: Cho khối lập phương có cạnh bằng 4. Thể tích của khối lập phương đã cho bằng:
-
A. 64
- B. 12
- C. 16
- D. 4
Câu 30: Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình dưới:

- A. (1+i)(2-i)
- B. (1+i)(2-3i)
-
C. $frac{3-2i}{i}$
- D. $frac{i}{2+3i}$
Câu 31: Cho $z_{1}, z_{2}$ là hai nghiệm phức của phương trình $z^{2}-2z+4=0$. Giá trị của biểu thức 3|$z_{1}$| – |$z_{2}$| bằng:
- A. 2$sqrt{3}$
- B. 6
- C. 4$sqrt{3}$
-
D. 4
Câu 32: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $Delta _{1}: frac{x+1}{1} = frac{y-2}{2} = frac{z+1}{3}$ và $Delta _{2}: frac{x+1}{1} = frac{y-2}{2} = frac{z+1}{-3}$. Đường thẳng d đi qua điểm (1;1;3) và vuông góc với cả hai đường thẳng $Delta _{1}, Delta _{2}$ có phương trình là:
- A. $left{begin{matrix}x=1+t y=1+t z=3+3tend{matrix}right.$
-
B. $left{begin{matrix}x=1+2t y=1-t z=3end{matrix}right.$
- C. $left{begin{matrix}x=-12+t y=6+t z=3tend{matrix}right.$
- D. $left{begin{matrix}x=1-2t y=1+t z=3-tend{matrix}right.$
Câu 33: Cho hàm số y = $x^{3}+3x$ có đồ thị (C). Tìm giao điểm của (C) và trục hoành:
- A. 2
- B. 3
- C. 0
-
D. 1
Câu 34: Trong không gian Oxyz, cho hai điểm A(1;-2;1) và B(-1;0;3). Phương trình mặt phẳng trung trực của đoạn AB là:
- A. -x+y+z-6=0
- B. x-y-z+4=0
-
C. x-y-z+1=0
- D. x-y-z-2=0
Câu 35: Tìm giá trị lớn nhất M của hàm số y = $x^{3}+2x^{2}-7x$ trên đoạn [0;4].
-
A. M = 68
- B. M = 13
- C. M = 70
- D. M = -4
Câu 36: Hàm số nào dưới đây đồng biến trên R
-
A. y = $x^{3}+3x$
- B. y = $-x^{2}+x$
- C. y = $frac{x+2}{x+4}$
- D. y = tanx
Câu 37: Cho $int_{1}^{e}frac{sqrt{3+lnx}}{x}dx = frac{a-bsqrt{3}}{3}$ với a, b là các số nguyên. Mệnh đề nào dưới đây đúng?
- A. a – 2b = 12
-
B. a – b = 10
- C. ab = 24
- D. a + b = 10
Câu 38: Cho tứ diện SABC có SA, SB, SC đôi một vuông góc. Biết SA = SB = a; SC = 2a. Tính khoảng cách từ điểm S đến mặt phẳng (ABC)
-
A. $frac{2a}{3}$
- B. $frac{a}{2}$
- C. $frac{asqrt{2}}{2}$
- D. $frac{2asqrt{5}}{5}$
Câu 39: Họ nguyên hàm của hàm số f(x) = 4x – cosx là:
- A. 4 + sinx + C
-
B. $2x^{2}$ – sinx + C
- C. $2x^{2}$ + sinx + C
- D. 4 – sinx + C
Câu 40: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): -x+y+3z-2=0. Phương trình mặt phẳng ($alpha $) đi qua A(2;-1;1) và song song với (P) là:
- A. x-y+3z-6=0
- B. -x+y-3z=0
-
C. -x+y+3z=0
- D. -x-y+3z=0
Câu 41: Trong không gian Oxyz, hình chiếu vuông góc của điểm M(3;-2;1) trên mặt phẳng (Oxz) có tọa độ là:
- A. (0;-2;1)
- B. (0;0;1)
-
C. (3;0;1)
- D. (3;-2;0)
Câu 42: Cho hàm số y = f(x) có bảng biến thiên như sau:

Hàm số đã cho đạt cực đại tại:
- A. x = -2
-
B. x = 0
- C. x = -1
- D. x = 3
Câu 43: Đường thẳng d đi qua điểm M(1;-2;1) và vuông góc với mặt phẳng x-2y+3z-4=0 có phương trình là:
- A. $frac{x-1}{1} = frac{y+2}{2} = frac{z-1}{-3}$
- B. $frac{x+1}{1} = frac{y-2}{-2} = frac{z-1}{3}$
-
C. $frac{x+1}{1} = frac{y-2}{-2} = frac{z+5}{3}$
- D. $frac{x-1}{1} = frac{y+2}{-2} = frac{z+1}{3}$
Câu 44: Cho số phức z thỏa mãn z(1-2i) + $bar{z}$i = 15 + i. Tìm mô đun của số phức z.
- A. |z| = 2$sqrt{5}$
-
B. |z| = 5
- C. |z| = 2$sqrt{3}$
- D. |z| = 4
Câu 45: Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số y = $-x^{3}-mx^{2}+(4m+9)x+5$ nghịch biến trên R.
-
A. 7
- B. 6
- C. 4
- D. 5
Câu 46: Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị như hình vẽ.

Gọi S là tập tất cả các giá trị nguyên của tham số m để phương trình f(sinx) = 2sinx + m có nghiệm trong khoảng (0;$pi $). Tính tổng các giá trị của S.
- A. -5
-
B. -6
- C. 10
- D. -3
Câu 47: Xét tất cả các số dương a và b thỏa mãn $log_{5}a = log_{125}(ab)$.Mệnh đề nào dưới đây đúng?
- A. $a = b^{2}$
- B. $a^{3} = b$
- C. a = b
-
D. $a^{2} = b$
Câu 48: Tập xác định D của hàm số y = $log_{2}(2x-1)$ là:
- A. D = ($-infty ;frac{1}{2}$)
- B. D = (0;$+infty $)
-
C. D = ($frac{1}{2};+infty $)
- D. D = ($frac{-1}{2};+infty $)
Câu 49: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quang của hình nón đỉnh S và đáy là hình tròn nội tiếp ABCD là:
- A. $frac{pi a^{2}sqrt{17}}{6}$
-
B. $frac{pi a^{2}sqrt{17}}{4}$
- C. $frac{pi a^{2}sqrt{17}}{8}$
- D. $frac{pi a^{2}sqrt{15}}{4}$
Câu 50: Cho hàm số f(x) có đạo hàm f'(x) = cosx và f(0) = 1. Giá trị $int_{0}^{pi }f(x)dx$ bằng:
- A. 0
- B. $pi $
- C. 2
-
D. 2 + $pi $
Chào mừng bạn đến với PRAIM, - nền tảng thông tin, hướng dẫn và kiến thức toàn diện hàng đầu! Chúng tôi cam kết mang đến cho bạn một trải nghiệm sâu sắc và tuyệt vời về kiến thức và cuộc sống. Với Praim, bạn sẽ luôn được cập nhật với những xu hướng, tin tức và kiến thức mới nhất.
- Chuyện cô giáo tận tụy gieo chữ trên đảo Trường Sa lớn
- Viết bài tập làm văn số 5 – Văn lập luận chứng minh (làm tại lớp)
- Nha khoa tiếng Anh là gì? Mổ xẻ ngữ nghĩa các từ về nha khoa
- Cách tạo app (ứng dụng) điện thoại qua 12 bước đơn giản
- My Clone Army: Trò chơi hấp dẫn đến từ vũ trụ của bản thân tôi

















