Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 1 môn Toán lớp 10 sách Kết nối tri thức năm 2023 – 2024. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 1 Toán 10. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 1 Toán 10 Kết nối tri thức bản word có lời giải chi tiết (chỉ 20k cho 1 đề thi bất kì):

B1: Gửi phí vào tài khoản 0711000255837 – NGUYEN THANH TUYEN – Ngân hàng Vietcombank

B2: Nhắn tin tới zalo Vietjack Official – nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi giữa kì 1 Toán lớp 10 Kết nối tri thức có đáp án năm 2023 – 2024 – Đề 1

Phòng Giáo dục và Đào tạo …..

Đề thi Giữa Học kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán 10

Thời gian làm bài: 90 phút

(Đề số 1)

I. PHẦN TRẮC NGHIỆM

Câu 1. Kí hiệu nào sau đây viết đúng mệnh đề: “5 không là số nguyên”

A. 5=Z B. 5∈Z

C. 5⊂Z D. 5∉Z

Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng?

A. ∀x∈R,x2>1⇒x>−1.

B. ∀x∈R,x2>1⇒x>1.

C. ∀x∈R,x>−1⇒x2>1.

D. ∀x∈R,x>1⇒x2>1

Câu 3. Cho A={n=2k|k∈N,k≤3} , B={n∈N|n≤5} và C={n∈N|2≤n≤6}.

Tìm tập hợp A∖(B∪C)

A. {0;8} B. {0}.

C. {8}. D. ∅.

Câu 4. Cho A=(−2;5] và B=(m;+∞). Tìm m∈Z để A∖B chứa đúng 5 số nguyên là:

A. 1. B. 3. C. 5 D. 7

Câu 5. Lớp 10A có 45 học sinh trong đó có 23 em thích môn Văn, 20 em thích môn Toán, 12 em không thích môn nào. Số em thích cả hai môn trên là :

A. 8. B. 10. C. 12. D. 14.

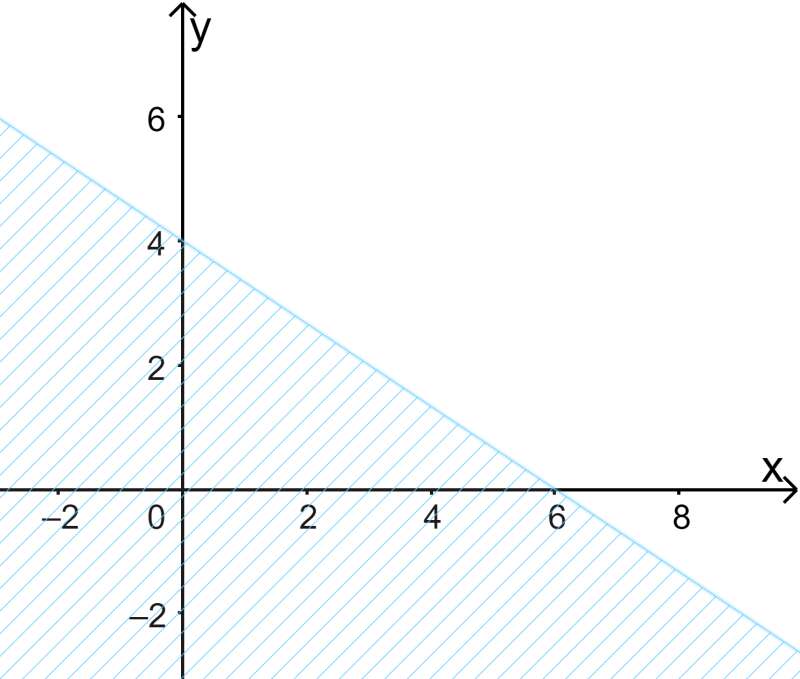
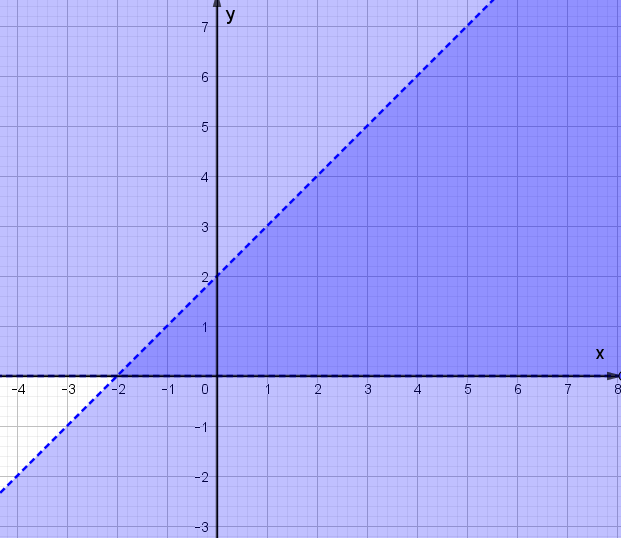
Câu 6. Miền nghiệm của bất phương trình 2x+3y≤12 là:

A. B.

C. D.

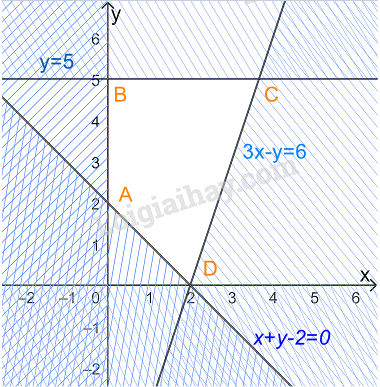
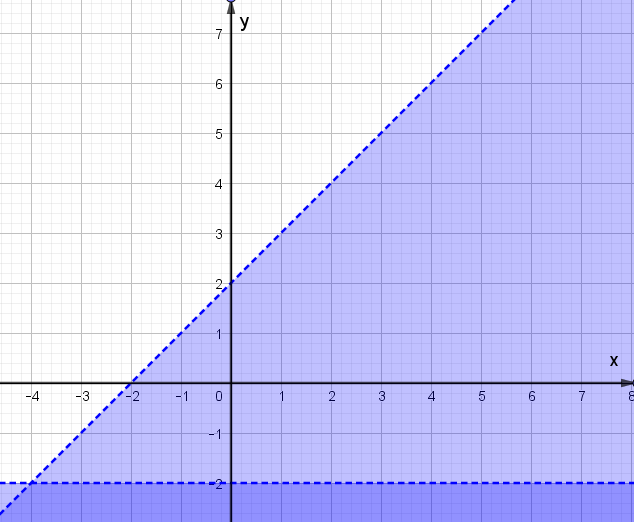
Câu 7. Giá trị lớn nhất của F(x;y)=5x−3y, với điều kiện {x≥00≤y≤5x+y−2≥03x−y≤6

A.−2 B. 10 C.103 D. −15

Câu 8. Cho góc x(0∘<x<180∘) thỏa mãn tan⁡x=5. Tính biểu thức P=3sin⁡x+11cos⁡x7sin⁡x−9cos⁡x

A. −2919. B. 2919. C. −1. D. 1.

Câu 9. Rút gọn biểu thức A=sin⁡x+sin⁡3x+sin⁡5xcos⁡x+cos⁡3x+cos⁡5x

A.sin⁡3x B. cos⁡3x. C. tan⁡3x. D. tan⁡x.

Câu 10. Cho tam giác ABC. Mệnh đề nào sau đây đúng?

A. sin⁡(A+B)=−sin⁡C B. sin⁡(A+B2)=cos⁡C2

C. cos⁡(A+B)=cos⁡C D. tan⁡(A+B)=tan⁡C

Câu 11. Cho tam giác ABC có BC=5,BAC^=120o. Bán kính đường tròn ngoại tiếp ΔABC bằng:

A.R=532 B. R=52

C. R=533 D. R=5

Câu 12. Cho tam giác ABC có c=4,b=7,A^=60∘. Chiều cao ha của tam giác ABC (làm tròn đến hàng đơn vị) là:

A. 2 B. 3 C. 4 D. 5

Câu 13. Điểm A(2;3) thuộc miền nghiệm của hệ bất phương trình nào dưới đây?

A. {x+2y>93x−y<5 B. {2x−y>7x+y≤3

C. {3x+5≤104x−y>3 D. {2x+5y>8x−3y≤4

Câu 14. Đơn giản biểu thức A=sin⁡(5π2−x)+cos⁡(13π+x)−3sin⁡(x−5π)

A. 3sin⁡x B. 3sin⁡x−cos⁡x C. −3sin⁡x. D. 2cos⁡x+3sin⁡x.

Câu 15. Cho bất phương trình 5(2x−3y)−3(2x−y+7)>x−3y. Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho?

A. O(0;0) B. A(1;0). C. B(3;−2). D. C(0;2)

II. PHẦN TỰ LUẬN

Câu 1. Xác định các tập hợp sau và biểu diễn chúng trên trục số.

a) (−∞;1)∩(−5;+∞) b) (2;6]∪(−3;5]

c) [−3;7)∖(4;+∞) d) R∖(−4;9]

Câu 2. Một xưởng nhỏ sản xuất hai loại sản phẩm A và B, mỗi cân sản phẩm loại A cần 2 cân nguyên liệu và 30 giờ sản xuất, mức lợi nhuận đem lại là 400 nghìn đồng/kg. Một cân sản phẩm loại B cần 4 cân nuyên liệu và 15 giờ sản xuất, mức lợi nhuận đem lại là 300 nghìn đồng. Mỗi ngày xưởng có 200 cân nguyên liệu và 1200 giờ làm việc. Vậy mỗi ngày xưởng đó nên sản xuất mỗi loại sản phẩm bao nhiêu kg để thu về mức lợi nhuận cao nhất?

Câu 3. Chứng minh rằng trong mọi tam giác ABC ta có:

a) a=b.cos⁡C+c.cos⁡B

b) ma2+mb2+mc2=34(a2+b2+c2)

Câu 4. Chứng minh trong mọi tam giác ABC ta đều có 1r=1ha+1hb+1hc

Hướng dẫn giải:

I. PHẦN TRẮC NGHIỆM

Câu 1:

Cách giải:

Tập hợp các số nguyên: Z

“5 không là số nguyên” viết là: 5∉Z

Chọn D.

Câu 2:

Cách giải:

Mệnh đề “∀x∈R,x2>1⇒x>−1” sai, chẳng hạn x=−3 thì x2>1 nhưng x<−1

Mệnh đề “∀x∈R,x2>1⇒x>1” sai, chẳng hạn x=−3 thì x2>1 nhưng x<1

Mệnh đề “∀x∈R,x>−1⇒x2>1” sai, chẳng hạn x=0>−1 nhưng x2<1

Mệnh đề “∀x∈R,x>1⇒x2>1” đúng

Chọn D.

Câu 3:

Phương pháp:

Liệt kê các phần tử của tập hợp A, B, C

Cách giải:

A={0;2;4;6;8}

B={0;1;2;3;4;5}

C={2;3;4;5;6}.

Ta có: B∪C={0;1;2;3;4;5;6}⇒A∖(B∪C)={0;8}

Chọn D.

Câu 4:

Cách giải:

+ Nếu m≥5 thì A∖B=(−2;5]∖(m;+∞)=A=(−2;5], chứa 7 số nguyên là -1 ; 0 ;1 ;2 ;3 ;4 ;5 (nhiều hơn 3) nên ta loại trường hợp m > 5.

+ Để A∖B≠∅ thì m>-2. Xét trường hợp -2<m<5, khi đó A∖B=(−2;5]∖(m;+∞)=(−2;m]

Chứa 5 số nguyên −1;0;1;2;3 thì m=3.

Chọn B.

Câu 5:

Cách giải:

Gọi X là tập hợp học sinh lớp 10A

A là tập hợp các học sinh thích môn Văn.

B là là tập hợp các học sinh thích môn Toán.

Suy ra :

A∩B là tập hợp các học sinh tham gia cả hai môn Văn và Toán.

A∪B là tập hợp các học sinh thích môn Văn và Toán.

X∖(A∪B) là tập hợp các học sinh không thích môn nào.

Ta có : n(A)=23;n(B)=20;n(X∖(A∪B))=12

⇒ Số học sinh thích môn Văn và Toán là:

n(A∪B)=45−12=33 (học sinh)

⇒ Số học sinh học sinh thích cả hai môn Văn và Toán là:

n(A∩B)=n(A)+n(B)−n(A∪B)=23+20−33=10 (học sinh)

Chọn B.

Câu 6:

Phương pháp:

Xác định đường thẳng 2x+3y=12 và xét một điểm (không thuộc đường thẳng) xem có thuộc miền nghiệm hay không.

Cách giải:

Đường thẳng 2x+3y=12 đi qua điểm có tọa độ (6;0) và (0;4) => Loại A, D.

Xét điểm O(0;0), ta có: 2.0+3.0=0<12 nên O thuộc miền nghiệm của BPT đã cho.

Chọn C.

Câu 7:

Phương pháp:

Bước 1: Biểu diễn miền nghiệm, xác định các đỉnh của miền nghiệm

Bước 2: Thay tọa độ các đỉnh vào F(x;y)=5x−3y, kết luận giá trị nhỏ nhất.

Cách giải:

Xét hệ bất phương trình {x≥00≤y≤5x+y−2≥03x−y≤6

Biểu diễn miền nghiệm của hệ, ta được

Miền nghiệm là miền tứ giác ABCD trong đó A(0;2),B(0;5),C(113;5),D(2;0)

Thay tọa độ các điểm A, B, C, D vào F(x;y)=5x−3y ta được

F(0;2)=5.0−3.2=−6

F(0;5)=5.0−3.5=−15

F(113;5)=5.113−3.5=103

F(2;0)=5.2−3.0=10

Vậy giá trị lớn nhất của F bằng 10.

Chọn B.

Câu 8:

Phương pháp:

Chia cả tử và mẫu của P cho cosx để làm xuất hiện tanx.

Cách giải:

Vì tan⁡x=5 nên cos⁡x≠0

Khi đó: P=3sin⁡x+11cos⁡x7sin⁡x−9cos⁡x=3sin⁡x+11cos⁡xcos⁡x7sin⁡x−9cos⁡xcos⁡x=3sin⁡xcos⁡x+117sin⁡xcos⁡x−9

=3tan⁡x+117tan⁡x−9=3.5+117.5−9=1

Chọn D.

Câu 9:

Phương pháp:

Áp dụng công thức:

sin⁡x+sin⁡5x=2sin⁡x+5x2cos⁡x−5×2

cos⁡x+cos⁡5x=2cos⁡x+5x2cos⁡x−5×2

Cách giải:

Ta có: sin⁡x+sin⁡5x=2sin⁡x+5x2cos⁡x−5×2=2sin⁡3xcos⁡(−2x)

cos⁡x+cos⁡5x=2cos⁡x+5x2cos⁡x−5×2=2cos⁡3xcos⁡(−2x)

⇒A=2sin⁡3xcos⁡(−2x)+sin⁡3x2cos⁡3xcos⁡(−2x)+cos⁡3x=sin⁡3x[2cos⁡(−2x)+1]cos⁡3x[2cos⁡(−2x)+1]=sin⁡3xcos⁡3x=tan⁡3x

Chọn C.

Câu 10:

Phương pháp

sin⁡(180∘−x)=sin⁡xcos⁡(180∘−x)=−cos⁡xtan⁡(180∘−x)=−tan⁡xsin⁡(90∘−x)=cos⁡x

Cách giải:

Ta có: A+B+C=180∘⇒{A+B=180∘−CA+B2=90∘−C2

Suy ra:

sin⁡(A+B)=sin⁡(180∘−C)=sin⁡C => Loại A

cos⁡(A+B)=cos⁡(180∘−C)=−cos⁡C => Loại B

tan⁡(A+B)=tan⁡(180∘−C)=−tan⁡C => Loại D

sin⁡(A+B2)=sin⁡(90∘−C2)=cos⁡C2

Chọn B.

Câu 11:

Phương pháp:

Áp dụng định lí sin: asin⁡A=2R

Cách giải:

Áp dụng định lí sin trong tam giác ABC, ta có: asin⁡A=2R

Mà a=BC=5,BAC^=120o

⇒R=a2sin⁡A=52sin⁡120∘=533

Chọn C.

Câu 12:

Phương pháp:

Áp dụng định lí cosin: a2=b2+c2−2bccos⁡A

Cách giải:

Ta có: c=4,b=7,A^=60∘

Áp dụng định lí cosin trong tam giác ABC ta có:

a2=b2+c2−2bccos⁡A

⇔a2=72+42−2.7.4cos⁡60∘=37⇒a=37

Lại có: S=12b.csin⁡A=12a.ha⇒ha=b.csin⁡Aa=7.4.sin⁡60∘37≈4

Vậy độ dài đường cao ha là khoảng 4.

Chọn C.

Câu 13.

Phương pháp:

Thay tọa độ điểm A vào hệ BPT, hệ nào cho ta các mệnh đề đúng thì điểm A thuộc miền nghiệm của hệ BPT đó.

Cách giải

+ Xét hệ {x+2y>93x−y<5, thay x=2,y=3 ta được: 2+2.3=8>9 sai nên A(2;3) không thuộc miền nghiệm của hệ BPT.

+ Xét hệ {2x−y>7x+y≤3, thay x=2,y=3 ta được: 2.2−3=1>7 sai nên A(2;3) không thuộc miền nghiệm của hệ BPT.

+ Xét hệ {3x+5≤104x−y>3, thay x=2,y=3 ta được: 3.2+5=11≤10 sai nên A(2;3) không thuộc miền nghiệm của hệ BPT.

+ Xét hệ {2x+5y>8x−3y≤4, thay x=2,y=3 ta được: {2.2+5.3=19>82−3.3=−7≤4 đúng nên A(2;3) thuộc miền nghiệm của hệ BPT.

Chọn D.

Câu 14.

Cách giải

Ta có:

sin⁡(5π2−x)=sin⁡(2π+π2−x)=sin⁡(π2−x)=cos⁡x

cos⁡(13π+x)=cos⁡(12π+x+π)=cos⁡(x+π)=−cos⁡x

sin⁡(x−5π)=sin⁡(x+π−6π)=sin⁡(x+π)=−sin⁡x

⇒A=cos⁡x+(−cos⁡x)−3(−sin⁡x)=3sin⁡x

Chọn A

Câu 15. Cho bất phương trình 5(2x−3y)−3(2x−y+7)>x−3y. Điểm nào dưới đây thuộc miền nghiệm của hệ đã cho?

A. O(0;0) B. A(1;0). C. B(3;−2). D. C(0;2)

Cách giải:

Ta có: 5(2x−3y)−3(2x−y+7)>x−3y

⇔10x−15y−6x+3y−21−x+3y>0⇔3x−9y−21>0⇔x−3y−7>0

Thay tọa độ các điểm vào BPT:

+ Vì 0−3.0−7=−7<0 nên O(0;0) không thuộc miền nghiệm

+ Vì 1−3.0−7=−6<0 nên A(1;0) không thuộc miền nghiệm

+ Vì 3−3.(−2)−7=2>0 nên B(3;−2) thuộc miền nghiệm

+ Vì 0−3.2−7=−13<0 nên C(0;2) không thuộc miền nghiệm

Chọn C

II. PHẦN TỰ LUẬN

Câu 1 (TH):

Phương pháp:

a) A∩B={x∈A|x∈B}

b) A∪B={x|x∈A hoặc x∈B}

c, d) A∖B={x∈A|x∉B}

Cách giải:

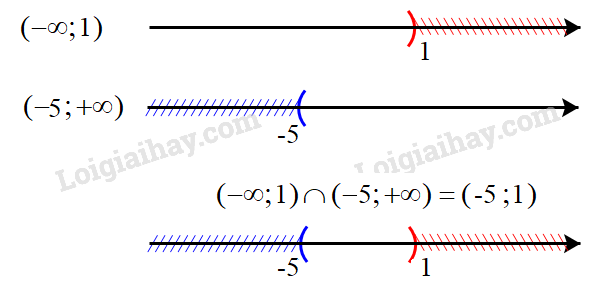
a) Biểu diễn hai tập (−∞;1) và (−5;+∞) trên trục số, ta được:

Giao của hai tập hợp: (−∞;1)∩(−5;+∞)=(−5;1)

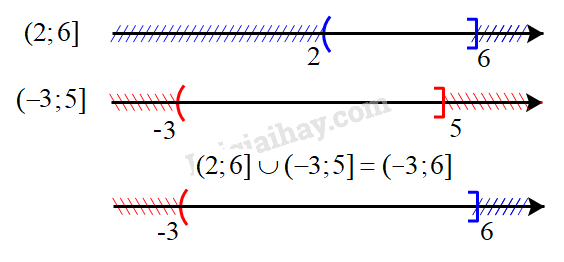
b) Biểu diễn hai tập (2;6] và (−3;5] trên trục số, ta được:

Hợp của hai tập hợp: (2;6]∪(−3;5]=(−3;6]

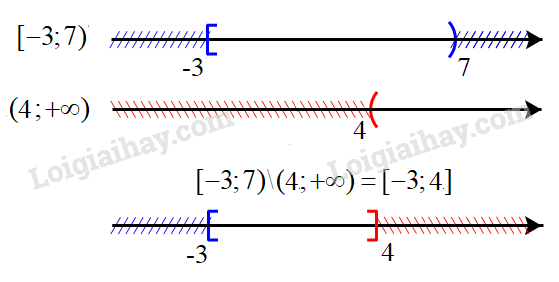
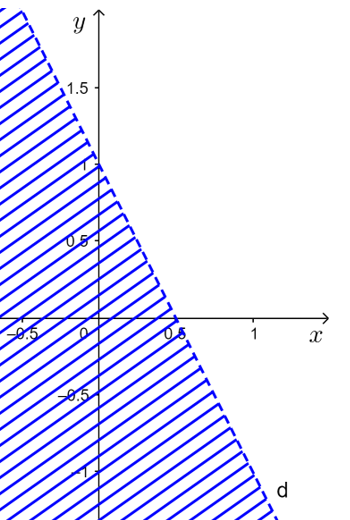
c) Biểu diễn hai tập (−3;7] và (4;+∞) trên trục số, ta được:

Hiệu của hai tập hợp: [−3;7)∖(4;+∞)=[−3;4]

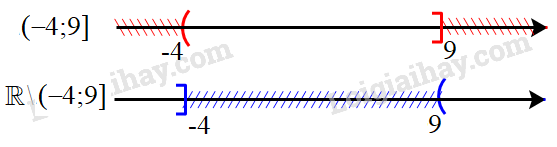
d) Biểu diễn tập (−4;9] trên trục số, ta được:

Hiệu của hai tập hợp: R∖(−4;9]=(−∞;−4]∪(9;+∞)

Câu 2:

Nhà cô Minh có mảnh vườn rộng 8m2. Cô dự định trồng cà chua và cải bắp trên toàn bộ mảnh vườn đó. Nếu trồng cà chua thì cần 20 công và thu được 300 nghìn đồng trên mỗi m2. Nếu trồng cải bắp thì cần 30 công và thu được 400 nghìn đồng trên mỗi m2. Hỏi cần cần trồng mỗi loại cây trên diện tích bao nhiêu để tthu được nhiều tiền nhất mà tổng số công không quá 180?

Cách giải:

Gọi số kg sản phẩm loại A, loại B cần sản xuất mỗi ngày lần lượt là x, y (x,y≥0)

Để sản xuất x kg sản phẩm loại A cần 2x cân nguyên liệu và 30x giờ sản xuất, lợi nhuận đem lại là 400x nghìn đồng

Để sản xuất y kg sản phẩm loại B cần 4y cân nguyên liệu và 15y giờ sản xuất, lợi nhuận đem lại là 300y nghìn đồng

Mỗi ngày có 200 kg nguyên liệu nên 2x+4y≤200

Có 1200 giờ làm việc nên 30x+15y≤1200

Tổng lợi nhuận đem lại là: F(x;y)=400x+300y

Ta có hệ bất phương trình: {x≥0y≥02x+4y≤20030x+15y≤1200

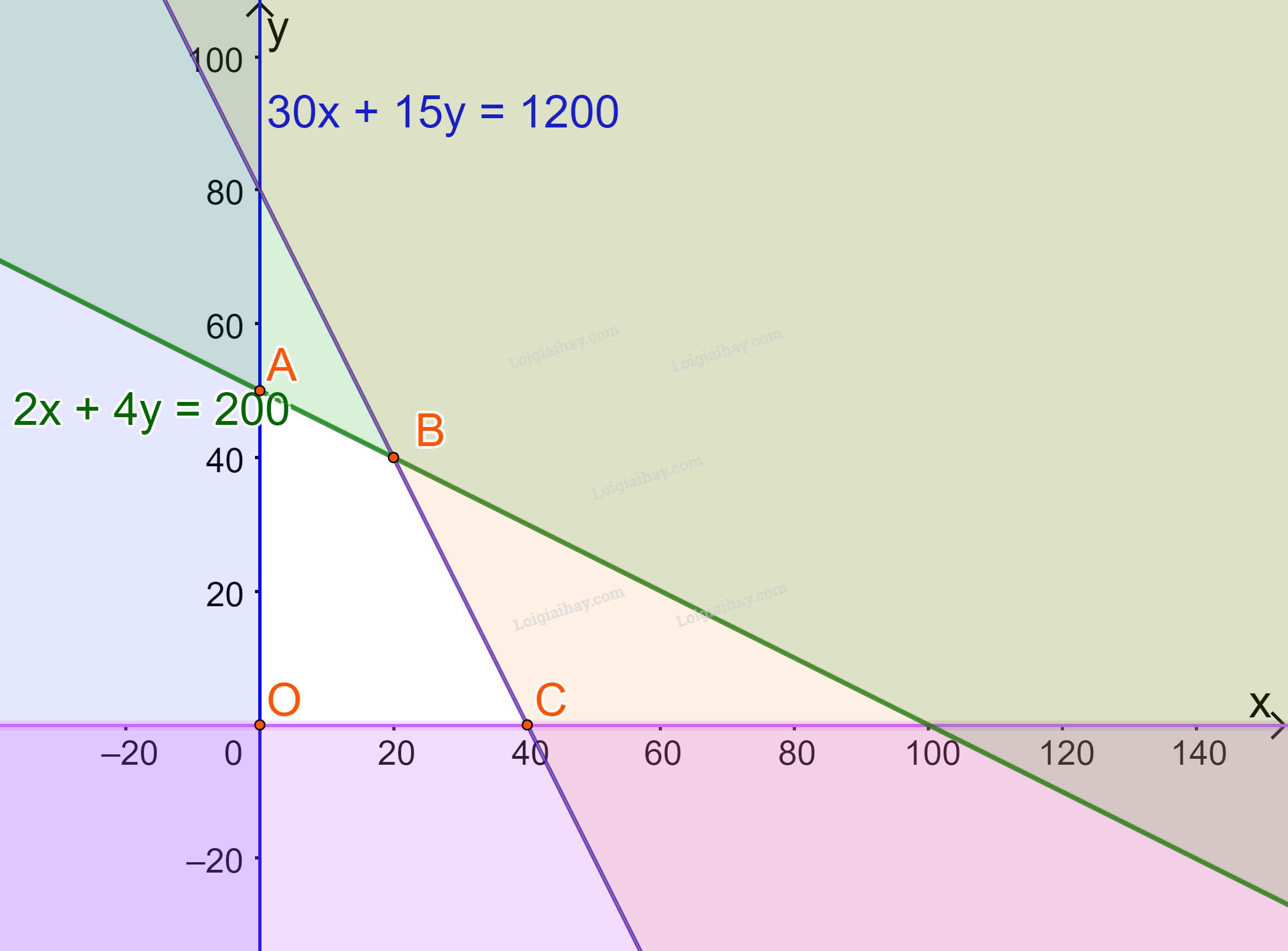
Biểu diễn miền nghiệm trên hệ trục Oxy, ta được:

Miền nghiệm là miền tứ giác OABC (kể cả các cạnh), trong đó A(0;50),B(20;40),C(40;0),O(0;0)

Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức F(x;y)=400x+300y ta được:

F(0;0)=400.0+300.0=0F(0;50)=400.0+300.50=15000F(20;40)=400.20+300.40=20000F(40;0)=400.40+300.0=16000

Do đó F đạt giá trị lớn nhất bằng 15 000 (nghìn đồng) tại x=20;y=40

Vậy mỗi ngày xưởng đó cần sản xuất 20kg sản phẩm loại A, 40kg sản phẩm loại B để thu về lợi nhuận lớn nhất.

Câu 3:

Phương pháp:

a) Áp dụng hệ quả của định lí cosin: cos⁡B=a2+c2−b22ac;cos⁡C=a2+b2−c22ab

b) Áp dụng các công thức tính diện tích:S=12a.ha=abc4R

Định lí sin: bsin⁡B=csin⁡C=2R

Cách giải:

a) Từ định lí cosin, ta suy ra:

cos⁡B=a2+c2−b22ac;cos⁡C=a2+b2−c22ab

⇒bcos⁡C+c.cos⁡B=b.a2+b2−c22ab+c.a2+c2−b22ac=a2+b2−c22a+a2+c2−b22a=a2+b2−c2+a2+c2−b22a=2a22a=a=12(2b2−2c2)=b2−c2

Vậy a=b.cos⁡C+c.cos⁡B

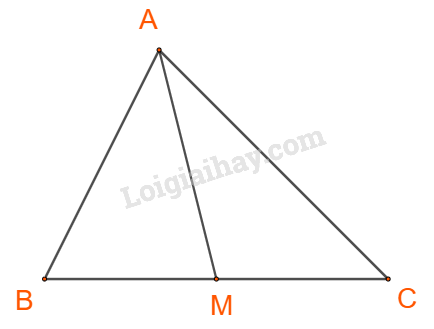
b) Gọi M là trung điểm BC. Khi đó AM=ma

Áp dụng định lí cosin trong tam giác ABM, ta có:

AM2=AB2+BM2−2.AB.BM.cos⁡B=c2+(a2)2−2.c.a2.cos⁡B=c2+a42−accos⁡B

Mà cos⁡B=a2+c2−b22ac,

suy ra ma2=c2+a42−ac.a2+c2−b22ac=c2+a42−a2+c2−b22=c2+b22−a42

Tương tự ta có: mb2=c2+a22−b42;mc2=b2+a22−c42

⇒ma2+mb2+mc2=c2+b22−a42+c2+a22−b42+b2+a22−c42=c22+c22−c24+b22+b22−b24+a22+a22−a24=3c24+3b24+3a24=34(a2+b2+c2)

Ta được điều phải chứng minh.

Câu 4:

Cách giải:

Xét tam giác ABC có a=BC,b=AC,c=AB

Ta có: S=12a.ha⇒ha=2Sa⇒1ha=a2S

Tương tự ta có: 1hb=b2S;1hc=c2S

⇒1ha+1hb+1hc=a2S+b2S+c2S=a+b+c2S

Lại có: S=pr=a+b+c2.r⇒r=2Sa+b+c⇒1r=a+b+c2S

Do đó 1r=1ha+1hb+1hc (đpcm)

Đề thi giữa kì 1 Toán lớp 10 Kết nối tri thức có đáp án năm 2023 – 2024 – Đề 2

Phòng Giáo dục và Đào tạo …..

Đề thi Giữa Học kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Môn: Toán 10

Thời gian làm bài: 90 phút

(Đề số 2)

I. Trắc nghiệm (7 điểm)

Câu 1. Trong các phát biểu sau, phát biểu nào không phải là mệnh đề?

A. 2 là số nguyên âm;

B. Bạn có thích học môn Toán không?;

C. 13 là số nguyên tố;

D. Số 15 chia hết cho 2.

Câu 2. Trong các tập hợp sau, tập hợp nào là con của tập hợp A = {1; 2; 3; 4; 5}?

A. A1 = {1; 6};

B. A2 = {0; 1; 3};

C. A3 = {4; 5};

D. A4 = {0}.

Câu 3. Cho các tập hợp A = {x ∈ ℝ | – 5 ≤ x < 1} và B = {x ∈ ℝ | – 3 < x ≤ 3}. Tìm tập hợp A ∪ B.

A. A ∪ B = [- 5; 1);

B. A ∪ B = [- 5; 3];

C. A ∪ B = (- 3; 1);

D. A ∪ B = (- 3; 3].

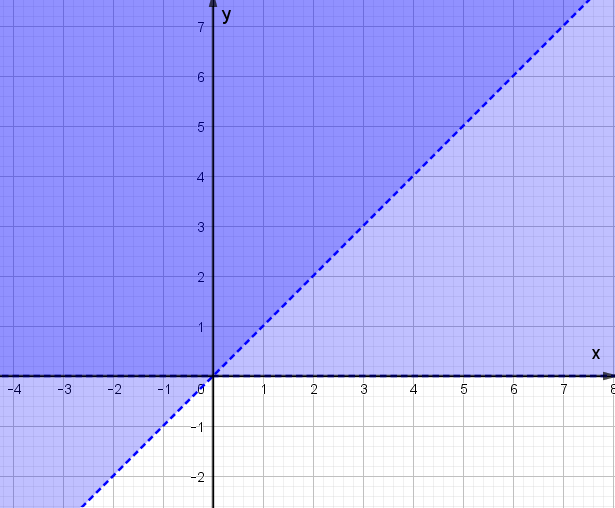
Câu 4. Nửa mặt phẳng không bị gạch chéo ở hình dưới đây là miền nghiệm của bất phương trình nào trong các bất phương trình sau?

A. x + 2y > 1;

B. 2x + y > 1;

C. 2x + y < 1;

D. 2x – y > 1.

Câu 5. Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình x+y−2≤02x−3y+2>0 ?

A. (0; 0);

B. (1; 1);

C. (- 1; 1);

D. (- 1; – 1).

Câu 6. Mệnh đề nào sau đây đúng?

A. sin (180° – α) = – sin α;

B. cos (180° – α) = – cos α;

C. tan (180° – α) = tan α;

D. cot (180° – α) = cot α);

Câu 7. Tam giác ABC có BC = 1, AC = 3, C^=60° . Tính độ dài cạnh AB.

A. 13 ;

B. 462 ;

C. 342 ;

D. 7 .

Câu 8. Cho hai mệnh đề P: “x là số chẵn” và Q: “x chia hết cho 2”.

Phát biểu mệnh đề P kéo theo Q.

A. Hoặc x là số chẵn hoặc x chia hết cho 2;

B. Nếu x là số chẵn thì x chia hết cho 2;

C. Nếu x chia hết cho 2 thì x là số chẵn;

D. x là số chẵn và x chia hết cho 2.

Câu 9. Trong các cặp số sau đây: (- 5; 0); (- 2; 1); (- 1; 3); (- 7; 0). Có bao nhiêu cặp số là nghiệm của bất phương trình x – 4y + 5 ≥ 0?

A. 0;

B. 1;

C. 3;

D. 4.

Câu 1. Giá trị của biểu thức P = sin30°.cos15° + sin150°.cos165° là

A. 0;

B. 1;

C. – 1;

D. 0,5.

Câu 11. Mệnh đề phủ định của mệnh đề P: “∃x, x2 + 2x + 3 là số chính phương” là:

A. ∀x, x2 + 2x + 3 không là số chính phương;

B. ∃x, x2 + 2x + 3 là số nguyên tố;

C. ∀x, x2 + 2x + 3 là hợp số;

D. ∃x, x2 + 2x + 3 là số thực.

Câu 12. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn ?

A. 2×2 + 1 ≥ y + 2×2;

B. 2x – 6y + 5 < 2x – 6y + 3;

C. 4×2 < 2x + 5y – 6;

D. 2×3 + 1 ≥ y + 2×2.

Câu 13. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Khẳng định nào dưới đây đúng?

A. a2 = b2 + c2 + 2bcsinA;

B. a2 = b2 + c2 – 2bccosA;

C. a2 = b2 + c2 – 2acsinA;

D. a2 = b2 + c2 + 2abcosA.

Câu 14. Cho tập hợp D = {x ∈ ℕ* | x(x – 2)(x – 3) = 0}.

Viết lại tập hợp D dưới dạng liệt kê các phần tử của tập hợp đó.

A. D = {0; 1; 2};

B. D = {2; 3};

C. D = {0; 2; 3};

D. D = {1; 2}.

Câu 15. Hệ nào là hệ bất phương trình bậc nhất hai ẩn trong các hệ sau?

Câu 16. Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. S là diện tích và p là nửa chu vi tam giác. R là bán kính đường tròn ngoại tiếp và r là bán kính đường tròn nội tiếp tam giác. Công thức nào sau đây sai?

A. S = abc4R ;

B. S = pr ;

C. S = p(p + a)(p + b)(p + c) ;

D. S = 12bcsinA.

Câu 17. Cho A⏜=45° , chọn đáp án SAI trong các đáp án dưới đây?

A. sin A = 32 ;

B. cos A = 22 ;

C. tan A = 1;

D. cot A = 1.

Câu 18. Cặp số nào sau đây là một nghiệm của bất phương trình: 3x + 2(y + 3) > 4(x + 1) – y + 3 ?

A. (-3; 0);

B. (3; 1);

C. (2; 1);

D. (0; 0).

Câu 19. Cho tập hợp B gồm các số tự nhiên bé hơn 20 và chia hết cho 4.

Viết tập hợp trên dưới dạng chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.

A. B = {x ∈ ℤ | x ≤ 20 và x ⁝ 4};

B. B = {x ∈ ℤ | x < 20 và x ⁝ 4};

C. B = {x ∈ ℕ | x ≤ 20 và x ⁝ 4};

D. B = {x ∈ ℕ | x < 20 và x ⁝ 4}.

Câu 20. Cho tam giác ABC biết sinBsinC=3 và AB=22 . Tính AC.

A. 22 ;

B. 23 ;

C. 26 ;

D. 25.

Câu 21. Cho tập hợp K = [1 ; 7) (- 3 ; 5). Khẳng định nào sau đây đúng ?

A. K = [1; 7);

B. K = (- 3; 7);

C. K = [1; 5);

D. K = [5; 7).

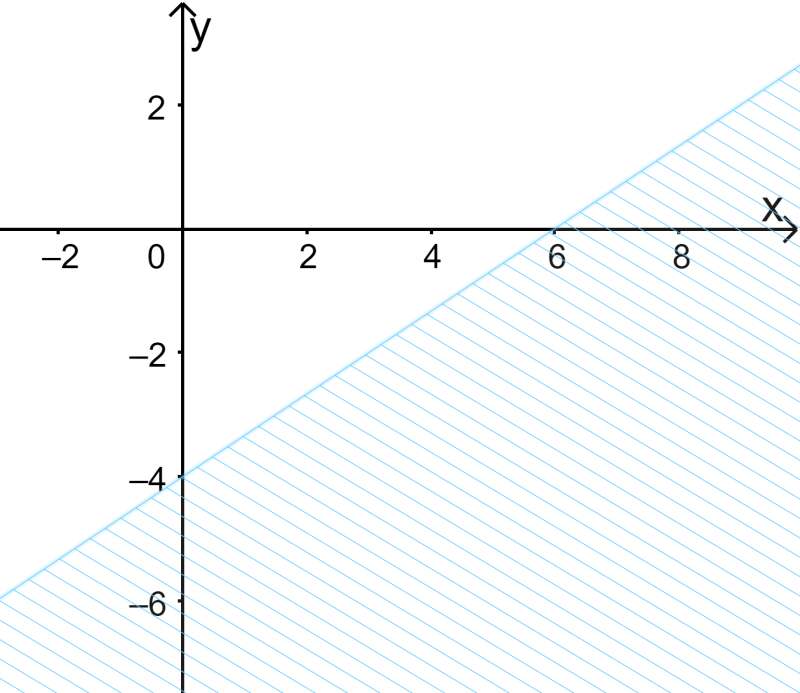
Câu 22. Miền nghiệm của hệ bất phương trình x-y+2>0y+2>0là phần màu trắng được biểu diễn trong hình vẽ nào dưới dây ?

A. ;

B. ;

C. ;

D. .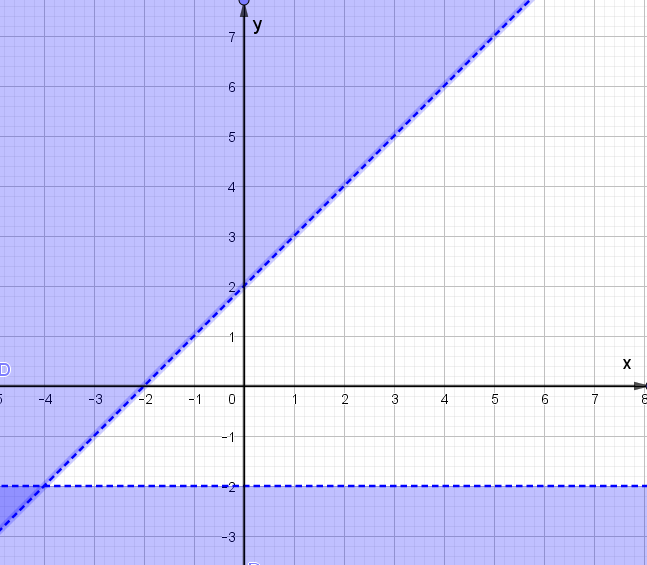

Câu 23. Cho hai nửa khoảng M = (0; 2], N = [1; 4). Tìm E = Cℝ(M ∩ N).

A. E = (0; 4);

B. E = [1; 2];

C. E = (- ∞; 1) ∪ (2; +∞);

D. E = (- ∞; 0] ∪ [4; +∞).

Câu 24. Cho mệnh đề: “Nếu tứ giác là một hình thoi thì tứ giác đó nội tiếp được một đường tròn”.

Mệnh đề đảo của mệnh đề trên là:

A. “Tứ giác là một hình thoi khi và chỉ khi tứ giác đó nội tiếp được trong một đường tròn”;

B. “Một tứ giác nội tiếp được trong một đường tròn khi và chỉ khi tứ giác đó là hình thoi”;

C. “Nếu một tứ giác nội tiếp được trong một đường tròn thì tứ giác đó là hình thoi”;

D. “Tứ giác là một hình thoi kéo theo tứ giác đó nội tiếp được trong một đường tròn”.

Câu 25. Cho tam giác ABC có AB = 4, AC = 8 và A⏜=30° . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

A. 7;

B. 6;

C. 5;

D. 4.

Câu 26. Cho góc α thỏa mãn cos2α=16 . Khẳng định nào sau đây là đúng?

A. 1 + cot2α = 6;

B. 1 + cot2α = 5;

C. 1 + tan2α = 5;

D. 1 + tan2α = 6.

Câu 27. Cho định lý sau: “Nếu hai tam giác bằng nhau thì hai tam giác đó đồng dạng”.

Phát biểu định lý trên dưới dạng điều kiện cần.

A. Hai tam giác bằng nhau kéo theo hai tam giác đó đồng dạng;

B. Hai tam giác bằng nhau là điều kiện cần để hai tam giác đó đồng dạng;

C. Hai tam giác đồng dạng là điều kiện cần để hai tam giác đó bằng nhau;

D. Hai tam giác bằng nhau tương đương với hai tam giác đó đồng dạng.

Câu 28. Miền nghiệm của bất phương trình x – 3y + 3 > 0 là:

A. Nửa mặt phẳng bờ là đường thẳng Δ: x – 3y + 3 = 0, không chứa gốc tọa độ O;

B. Nửa mặt phẳng bờ là đường thẳng Δ: x – 3y + 3 = 0 (không kể bờ), không chứa gốc tọa độ O;

C. Nửa mặt phẳng bờ là đường thẳng Δ: x – 3y + 3 = 0, chứa gốc tọa độ O;

D. Nửa mặt phẳng bờ là đường thẳng Δ: x – 3y + 3 = 0 (không kể bờ), chứa gốc tọa độ O.

Câu 29. Cho các mệnh đề dưới đây:

(1) 24 là số nguyên tố.

(2) Phương trình x2 – 5x + 9 = 0 có 2 nghiệm thực phân biệt.

(3) Phương trình x2 + 1 = 0 có 2 nghiệm thực phân biệt.

(4) Mọi số nguyên lẻ đều không chia hết cho 2.

Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?

A. 1;

B. 2;

C. 3;

D. 4.

Câu 30. Bạn Vân có tối đa 120 phút để trồng rau trong vườn. Biết có hai loại rau là rau cải và rau muống, một cây rau cải trồng mất 5 phút, một cây rau muống trồng mất 7 phút. Gọi số cây rau cải bạn Vân trồng được là x cây, số cây rau muống bạn Vân trồng được là y cây. Các bất phương trình mô tả điều kiện của bài toán là:

A. 7x + 5y ≥ 120; x > 0; y > 0;

B. 5x + 7y ≤ 120; x ≥ 0; y ≥ 0;

C. 7x + 5y > 120; x > 0; y > 0;

D. 7x + 5y < 120; x < 0; y > 0.

Câu 31. Cho tam giác ABC. Xét dấu của biểu thức P = cosA2. sin B?

A. P > 0;

B. P < 0;

C. P = 0;

D. Một kết quả khác.

Câu 32. Để xác định chiều cao của một tòa tháp mà không cần lên đỉnh của tòa nhà người ta làm như sau: đặt giác kế thẳng đứng cách chân tháp một khoảng AB = 55 m, chiều cao của giác kế là OA = 2 m.

Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh C của tháp. Đọc trên giác kế số đo góc COD^=60° .

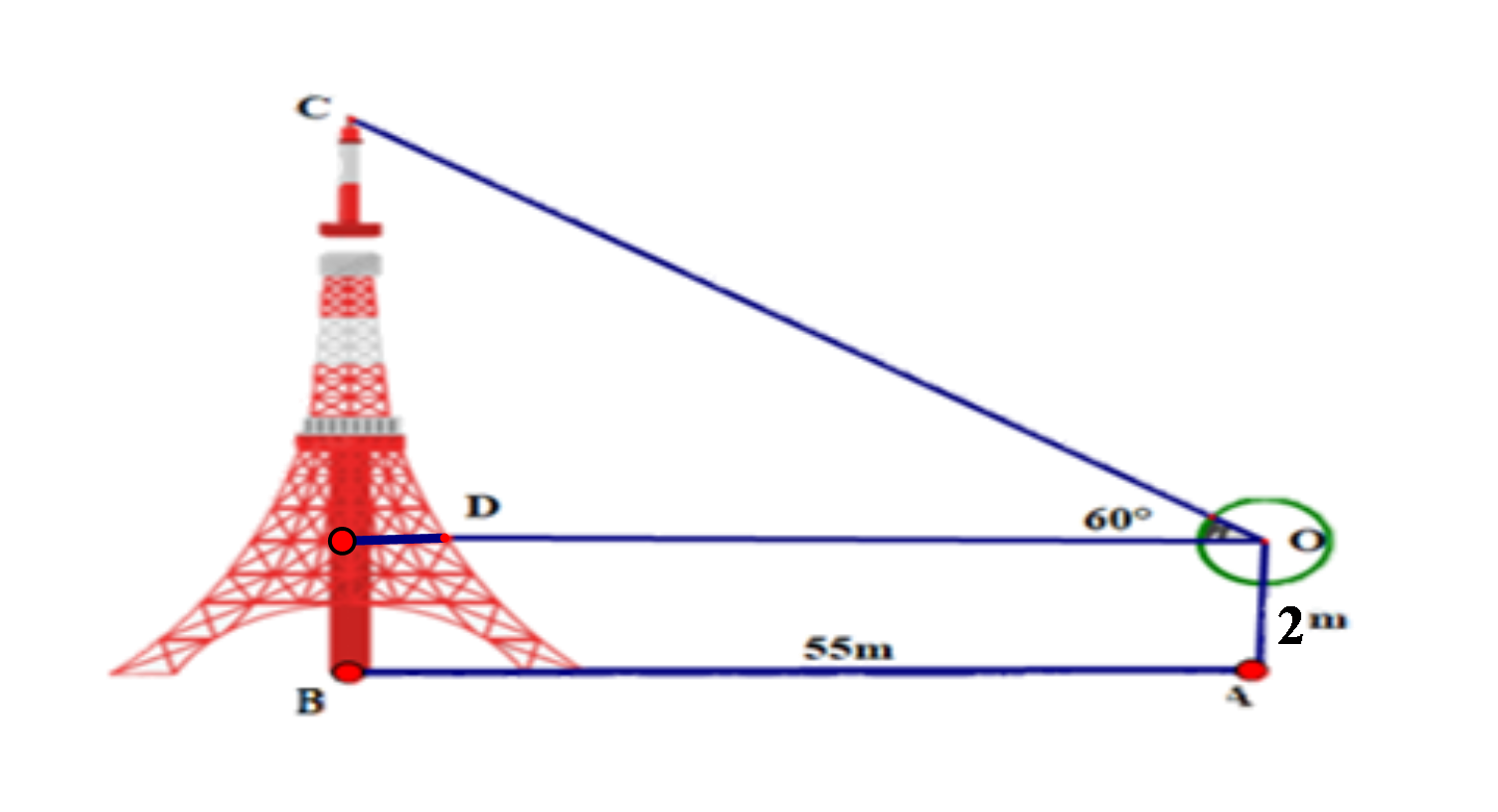
Chiều cao của ngọn tháo gần nhất với giá trị nào sau đây?

A. 87 m;

B. 90 m;

C. 97 m;

D. 100 m.

Câu 33. Cho góc α với 0° < α < 180°. Tính giá trị của cosα, biết tanα=−22.

A. −13 ;

B. 223 ;

C. 13 ;

D. 23 .

Câu 34. Miền nghiệm của hệ bất phương trình 2x+3y−15<0x+y>0chứa điểm nào trong các điểm sau đây ?

A. (1; 15);

B. (7; 8);

C. (9; 11);

D. (1; 2).

Câu 35. Cho tam giác ABC có AB = 5 , A^=30°, B^=75°. Tính diện tích tam giác ABC.

A. ;

B. 4;

C. ;

D. 5.

II. Tự luận (3 điểm)

Câu 1. Cho hai tập hợp A = (0; 3), B = (2; 4). Xác định các tập hợp A ∪ B, A ∩ B, A B và CℝA.

Câu 2. Một phân xưởng có hai máy đặc chủng loại 1 và loại 2 sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy loại 1 trong 3 giờ và máy loại 2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy loại 1 trong 1 giờ và máy loại 2 trong 1 giờ. Máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày. Hỏi cần sản xuất bao nhiêu tấn sản phẩm loại A và loại B để số tiền lãi mà phân xưởng này có thể thu được trong một ngày là lớn nhất?

Câu 3. Cho tam giác ABC. Chứng minh rằng:

sin A = sin B . cos C + sin C . cos B.

ĐÁP ÁN ĐỀ SỐ 2

I. Bảng đáp án trắc nghiệm

II. Hướng dẫn giải chi tiết trắc nghiệm

Câu 1.

Đáp án đúng là: B

Phát biểu “Bạn có thích học môn Toán không?” là một câu hỏi, không khẳng định tính đúng sai nên đây không phải mệnh đề.

Câu 2.

Đáp án đúng là: C

Tập con của tập hợp A là tập hợp gồm các phần tử đều là phần tử của tập hợp A.

Tập A1 = {1; 6} không là tập con của tập A vì 6 ∉ A.

Tập A2 = {0; 1; 3} không là tập con của tập A vì 0 ∉ A.

Tập A3 = {4; 5} là tập con của tập A vì 4 ∈ A, 5 ∈ A.

Tập A4 = {0} không là tập con của tập A vì 0 ∉ A.

Vậy chỉ có tập A3 là tập con của tập A.

Câu 3.

Đáp án đúng là: B

Ta có: A = {x ∈ ℝ | – 5 ≤ x < 1} = [- 5; 1)

Và B = {x ∈ ℝ | – 3 < x ≤ 3} = (- 3; 3].

Do đó, A ∪ B = {x | x ∈ A hoặc x ∈ B} = [- 5; 3].

Câu 4.

Đáp án đúng là: B

Giả sử đường thẳng d có phương trình: y = ax + b.

Từ hình vẽ ta thấy, đường thẳng d đi qua hai điểm có tọa độ (0; 1) và (0,5; 0).

Khi đó ta có hệ a.0+b=1a.0,5+b=0⇔a=−2b=1 .

Do đó, d: y = – 2x + 1 hay d: 2x + y = 1.

Lấy điểm O(0; 0) không thuộc đường thẳng d, ta thấy 2 . 0 + 0 = 0 < 1 và nửa mặt phẳng không bị gạch chéo không chứa điểm O.

Vậy nửa mặt phẳng không bị gạch chéo ở hình đã cho là miền nghiệm của bất phương trình 2x + y > 1.

Câu 5.

Đáp án đúng là: C

Thay lần lượt các cặp số vào hệ bất phương trình x+y−2≤02x−3y+2>0 ta thấy chỉ có cặp số (- 1; 1) không thỏa mãn, do cặp số này không thỏa mãn bất phương trình thứ hai của hệ (2 . (- 1) – 3 . 1 + 2 = – 3 < 0).

Vậy trong các cặp số đã cho, cặp số (- 1; 1) không là nghiệm của hệ bất phương trình đã cho.

Câu 6.

Đáp án đúng là: B

Hai góc bù nhau thì sin bằng nhau, côsin, tang và côtang đối nhau.

Do đó, sin (180° – α) = sin α; cos (180° – α) = – cos α;

tan (180° – α) = – tan α; cot (180° – α) = – cot α).

Vậy trong các đáp án đã cho, đáp án đúng là đáp án B.

Câu 7.

Đáp án đúng là: D

Áp dụng định lí côsin trong tam giác ABC ta có:

AB2 = BC2 + AC2 – 2 BC. AC . cosC = 12 + 32 – 2 . 1 . 3 . cos 60° = 7.

Suy ra AB = 7 .

Câu 8.

Đáp án đúng là: B

Vì mệnh đề kéo theo được phát biểu dưới dạng là “Nếu P thì Q”.

Nên mệnh đề P kéo theo Q là “Nếu x là số chẵn thì x chia hết cho 2”.

Câu 9.

Đáp án đúng là: B

Ta có:

– 5 – 4.0 + 5 = 0, vậy (- 5; 0) là nghiệm của bất phương trình.

– 2 – 4.1 + 5 = – 1 < 0, vậy (- 2; 1) không là nghiệm của bất phương trình.

– 1 – 4.3 + 5 = – 8 < 0, vậy (- 1; 3) không là nghiệm của bất phương trình.

– 7 – 4.0 + 5 = – 2 < 0, vậy (-7; 0) không là nghiệm của bất phương trình.

Vậy có 1 cặp số là nghiệm của bất phương trình.

Câu 10.

Đáp án đúng là: A

Sử dụng công thức: sin (180° – α) = sin α và cos (180° – α) = – cos α.

Ta có: sin 30° = sin150°; cos15° = – cos165°

P = sin30°.cos15° + sin150°.cos165° = sin30°.cos15° – sin30°.cos15° = 0.

Câu 11.

Đáp án đúng là: A