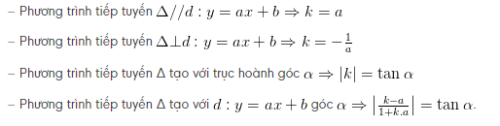Công thức đạo hàm log, logarit, căn bậc 3, căn x, lượng giác

Hàm số logarit và công thức tính đạo hàm log là những nội dung cực kỳ quan trọng trong chương trình Toán 12. Đây là những kiến thức tối quan trọng và thường xuất hiện trong các đề thi. Vì vậy, trong bài viết này, PRAIM sẽ tổng hợp lại những kiến thức cơ bản về hàm logarit, công thức tính đạo hàm log, cùng với những ví dụ minh họa dễ hiểu để giúp các bạn nắm chắc phần kiến thức này.

1. Tổng hợp các công thức đạo hàm

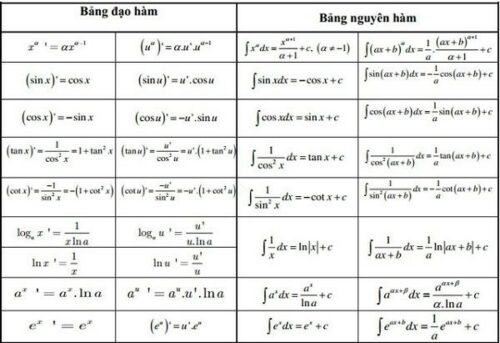
Quy tắc cơ bản của đạo hàm được thể hiện trong bảng dưới đây:

2. Bảng đạo hàm lượng giác

Bảng đạo hàm lượng giác giúp chúng ta tính được đạo hàm của các hàm số lượng giác một cách nhanh chóng:

3. Công thức đạo hàm logarit

Công thức đạo hàm logarit giúp chúng ta tính được đạo hàm của hàm số logarit một cách dễ dàng:

4. Công thức đạo hàm số mũ

Công thức đạo hàm số mũ giúp chúng ta tính được đạo hàm của hàm số mũ một cách thuận tiện:

5. Công thức đạo hàm log

Công thức đạo hàm log giúp chúng ta tính được đạo hàm của hàm số log một cách dễ dàng:

6. Bảng đạo hàm và nguyên hàm

Bảng đạo hàm và nguyên hàm cung cấp cho chúng ta thông tin về đạo hàm và nguyên hàm của một số hàm số quan trọng:

7. Các dạng bài toán về công thức đạo hàm

7.1 Tính đạo hàm bằng định nghĩa

Hàm số y = f(x) có đạo hàm tại điểm x = x khi và chỉ khi f'(x)=f'(x).

Ví dụ: f(x) = 2x +1 tại x=2

7. 2 Chứng minh các đẳng thức về đạo hàm

Ví dụ: Cho y = e.sinx, chứng minh hệ thức y”+2y′+ 2y = 0

Bài giải:

Ta có y′=−e.sinx + e.cosx

y′ =−e.sinx+e−x.cosx

y”=e.sinx−e.cosx−e.cosx−e.sinx = −2e.cosx

Vậy y”+ 2y′+ 2y = −2.e.cosx− −2.e.sinx + 2.e.cosx + 2.e.sinx =0

7.3 Viết phương trình tiếp tuyến khi biết tiếp điểm

Phương trình tiếp tuyến của đường cong (C): y= f(x) tại tiếp điểm M(x, y) có dạng:

Ví dụ: Cho hàm số y= x +3mx + ( m+1)x + 1 (1), m là tham số thực. Tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số (1) tại điểm có hoành độ x = -1 đi qua điểm A(1,2).

Tập xác định D = R

y’ = f'(x) = 3x + 6mx + m + 1

Với x = -1 => y = 2m -1, f'(-1) = -5m + 4

Phương trình tiếp tuyến tại điểm M(-1, 2m – 1): y = (-5m + 4)(x + 1) + 2m – 1 (d)

Ta có A(1,2) ∈ (d) <=> (-5m + 4)2 + 2m – 1 = 2 => m = 5/8

7.4 Viết phương trình tiếp khi biết hệ số góc

Viết phương trình tiếp tuyến Δ của ( C ): y = f(x), biết Δ có hệ số góc k cho trước

Gọi M(x, y) là tiếp điểm. Tính y’ => y'(x)

Do phương trình tiếp tuyến Δ có hệ số góc k => y’ = (x) = k (i)

Giải (i) tìm được x => y = f(x) => Δ: y = k(x – x) + y

Lưu ý: Hệ số góc k = y'(x) của tiếp tuyến Δ thường được tính như sau:

Ví dụ: Cho hàm số y=x +3x -9x+5 ( C). Trong tất cả các tiếp tuyến của đồ thị ( C ), hãy tìm tiếp tuyến có hệ số góc nhỏ nhất.

Ta có y’ = f'(x) = 3x + 6x – 9

Gọi x là hoành độ tiếp điểm của tiếp tuyến, vậy f'(x) = 3 x + 6 x – 9

Ta có 3 x + 6 x – 9 =3 ( x + 2x +1) – 12 = 3 (x +1) – 12 > – 12

Vậy min f(x) = – 12 tại x = -1 => y = 16

Suy ra phương trình tiếp tuyến cần tìm: y= -12( x+1)+16 <=> y= -12x + 4

7.5 Phương trình và bất phương trình có đạo hàm

Tham khảo ngay các khoá học online của PRAIM

Đội ngũ PRAIM vừa chia sẻ những kiến thức quan trọng về hàm số logarit cũng như công thức tính đạo hàm log. Hy vọng rằng bài viết này sẽ giúp các bạn nắm vững những kiến thức căn bản để học Toán tốt hơn và đạt điểm cao trong các kỳ thi sắp tới. Để học trực tuyến online nhiều nội dung hơn, hãy đồng hành cùng PRAIM mỗi ngày. Chúc các bạn thành công!

PRAIM