Thể tích hình hình lập phương là một trong những công thức toán học quan trọng, đặc biệt là đối với các bạn học sinh lớp 5. Vậy hình lập phương là gì và cách tính thể tích của hình lập phương ra sao? Hãy cùng INVERT tìm hiểu và giải đáp thắc mắc thông qua bài viết sau.

Hình lập phương là gì? Thể tích hình lập phương là gì?
Hình lập phương (khối lập phương) là 1 khối đa diện đều 3 chiều có 6 mặt đều là hình vuông, 12 cạnh bằng nhau, 8 đỉnh, cứ 3 cạnh gặp nhau tại 1 đỉnh và có 4 đường chéo cắt nhau tại 1 điểm. Khối lập phương là tập hợp những điểm nằm bên trong và các điểm nằm trên các mặt, cạnh, đỉnh này.
Bên cạnh đó, khối lập phương là khối 6 mặt đều duy nhất và là 1 trong 5 khối đa diện đều với 9 mặt đối xứng. Hình lập phương cũng là hình khối lục diện vuông, hình hộp chữ nhật có các cạnh bằng nhau hoặc hình khối mặt thoi vuông.
Thể tích hình lập phương xác định là số đơn vị khối, chiếm hoàn toàn bởi hình lập phương.
Tính chất của hình lập phương
- Có 8 mặt phẳng đối xứng
- Có 12 cạnh bằng nhau, 8 đỉnh, cứ 3 cạnh gặp nhau tại một đỉnh
- Có 4 đường chéo cắt ngang tại 1 điểm, là tâm đối xứng của hình lập phương.
- Đường chéo các mặt bên của khối lập phương đều dài bằng nhau
- Đường chéo của hình lập phương cũng dài bằng nhau.
Công thức tính thể tích hình lập phương
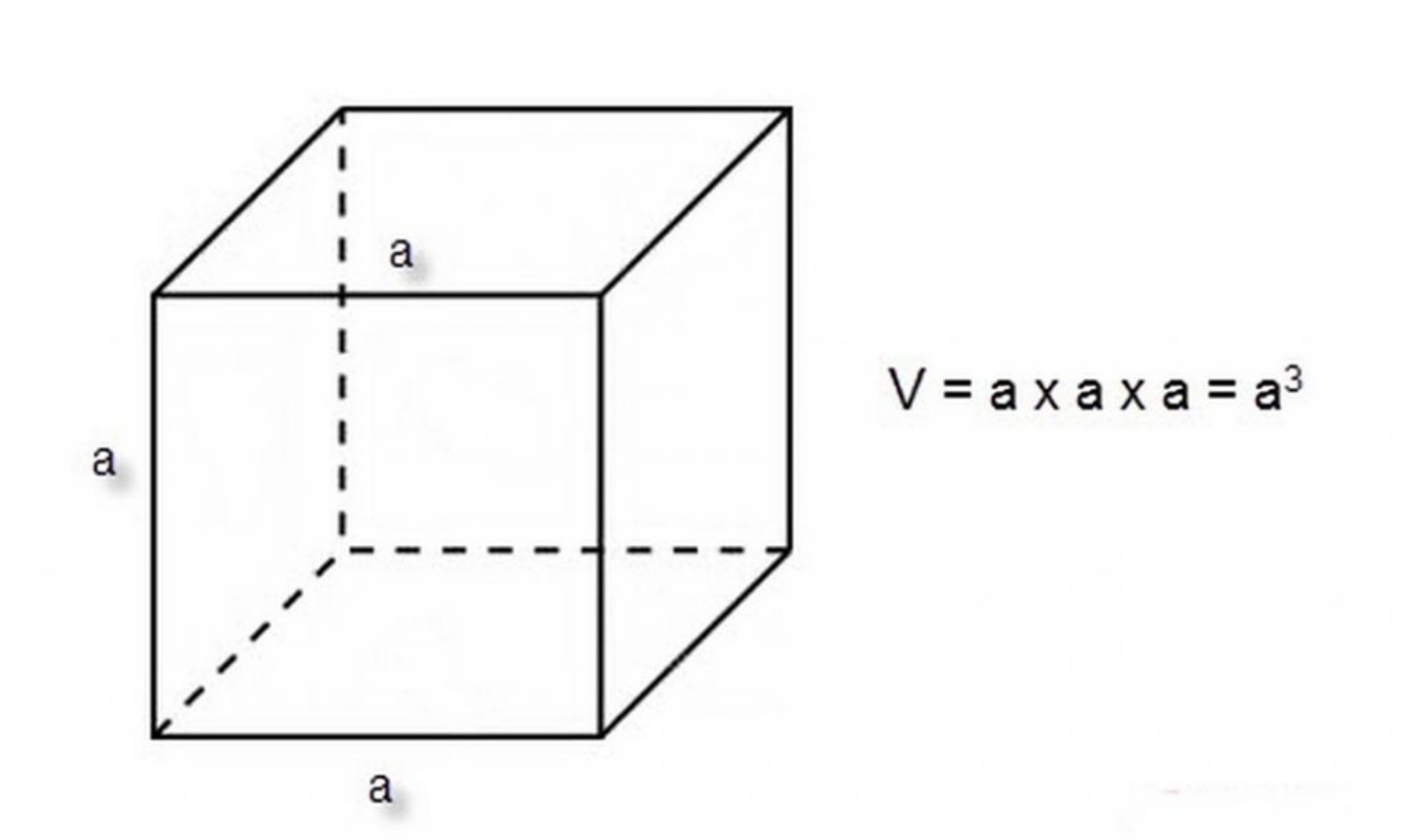
Thể tích hình lập phương được tính bằng cạnh nhân với cạnh rồi nhân với cạnh.
Trong đó:
- V: thể tích của hình lập phương
- a: độ dài cạnh của hình lập phương
- Đơn vị thể tích: m3 (mét khối)
Hướng dẫn giải bài tập tìm thể tích khối lập phương
Dạng 1: Tính thể tích hình lập phương khi biết độ dài
Phương pháp: Muốn tính thể tích hình lập phương, lấy cạnh nhân với cạnh rồi nhân với cạnh.
Dạng 2: Tính thể tích khối lập phương khi biết diện tích xung quanh hoặc diện tích toàn phần
Phương pháp: Tính diện tích một mặt, sau đó lập luận để tìm được độ dài của cạnh. Từ đó, có thể tính thể tích hình lập phương lớp 5.
Dạng 3: Tính độ dài cạnh khi biết thể tích
Phương pháp: Nếu tìm một số a mà a x a x a = V thì độ dài cạnh hình lập phương là a
Dạng 4: So sánh thể tích của một hình lập phương với thể tích của một hình chữ nhật hoặc một hình lập phương khác
Phương pháp: Áp dụng công thức để tính thể tích từng hình rồi so sánh
Dạng 5: Toán có lời văn
Phương pháp: Đọc kỹ đề bài, xác định dạng Toán và yêu cầu của đề bài rồi giải bài toán đó.
Hướng dẫn cách tính thể tích hình lập phương
1. Tìm lũy thừa bậc ba 1 cạnh của hình lập phương
Bước 1: Tìm chiều dài của 1 cạnh hình lập phương
Thường thì đề bài sẽ cho sẵn độ dài 1 cạnh để bạn có thể dễ dàng tính được thể tích hình lập phương. Tuy nhiên, trong một số trường hợp yêu cầu tìm thể tích 1 vật có thực hình lập phương, bạn hãy dùng thước kẻ hay thước cuộn để đo cạnh hình lập phương đó.
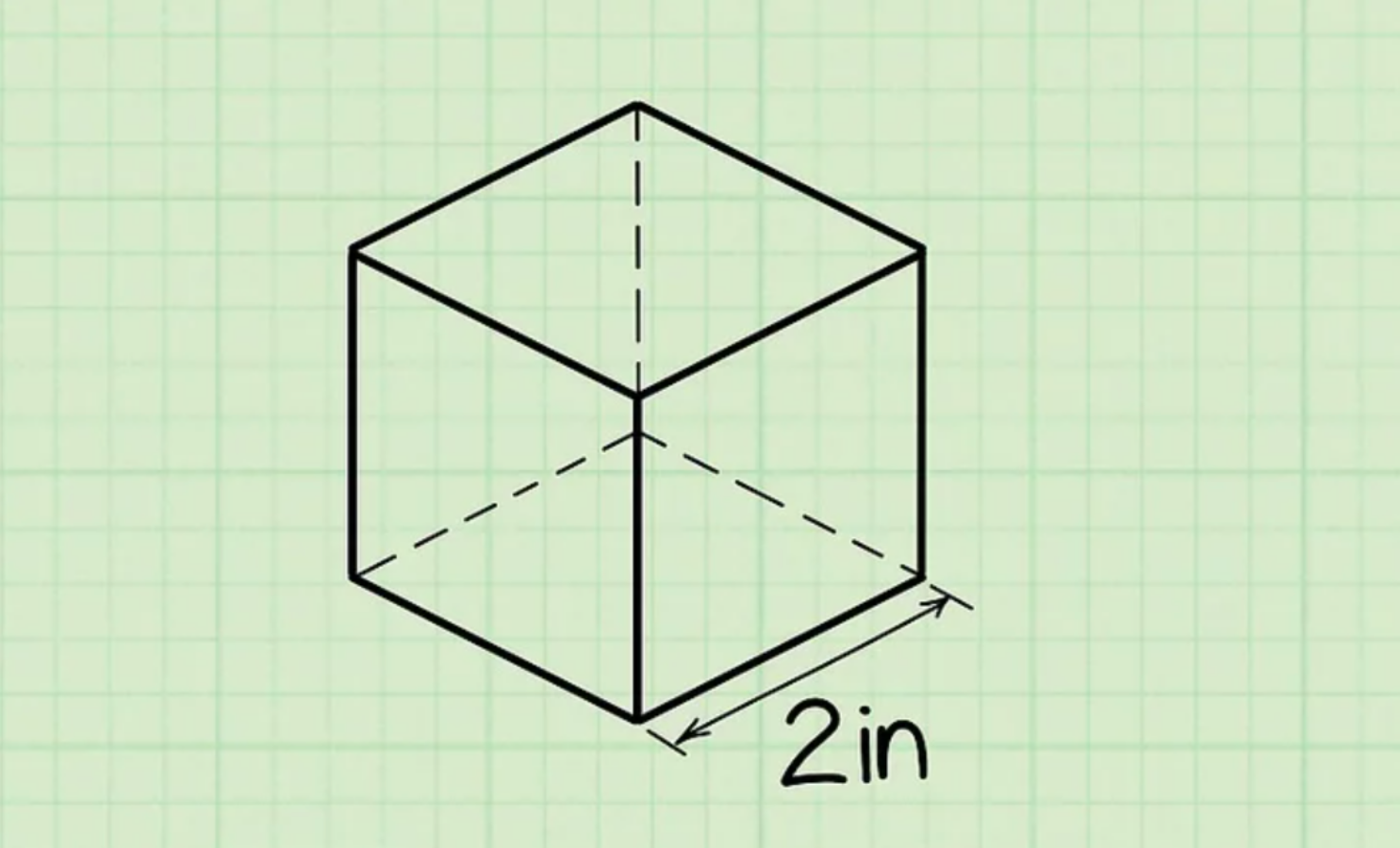
Bước 2: Lũy thừa bậc 3 độ dài cạnh
Khi đã tìm ra độ dài cạnh hình lập phương, bạn tiến hành lũy thừa bậc 3 con số này lên. Hay nhân số này với chính nó 2 lần. Nếu s là độ dài cạnh, công thức thể tích của hình lập phương là s × s × s.
Hay nói cách khác thể tích hình lập phương sẽ bằng chiều dài × chiều rộng × chiều cao và bằng lũy thừa bậc 3 độ dài của cạnh bất kỳ.

Bước 3: Đánh dấu đáp án của bạn với ký hiệu mũ 3
Vì thể tích là đơn vị đo không gian ba chiều, nên đáp án của bạn phải ở dạng mũ 3. Đừng quên dùng đúng đơn vị để không bị trừ điểm nhé!
ì đơn vị đo ban đầu là cm, đáp án cuối cùng sẽ phải ghi theo đơn vị “cm khối” (hoặc cm3). Vì thế, đáp án 8 của chúng ta sẽ trở thành 8 cm3.
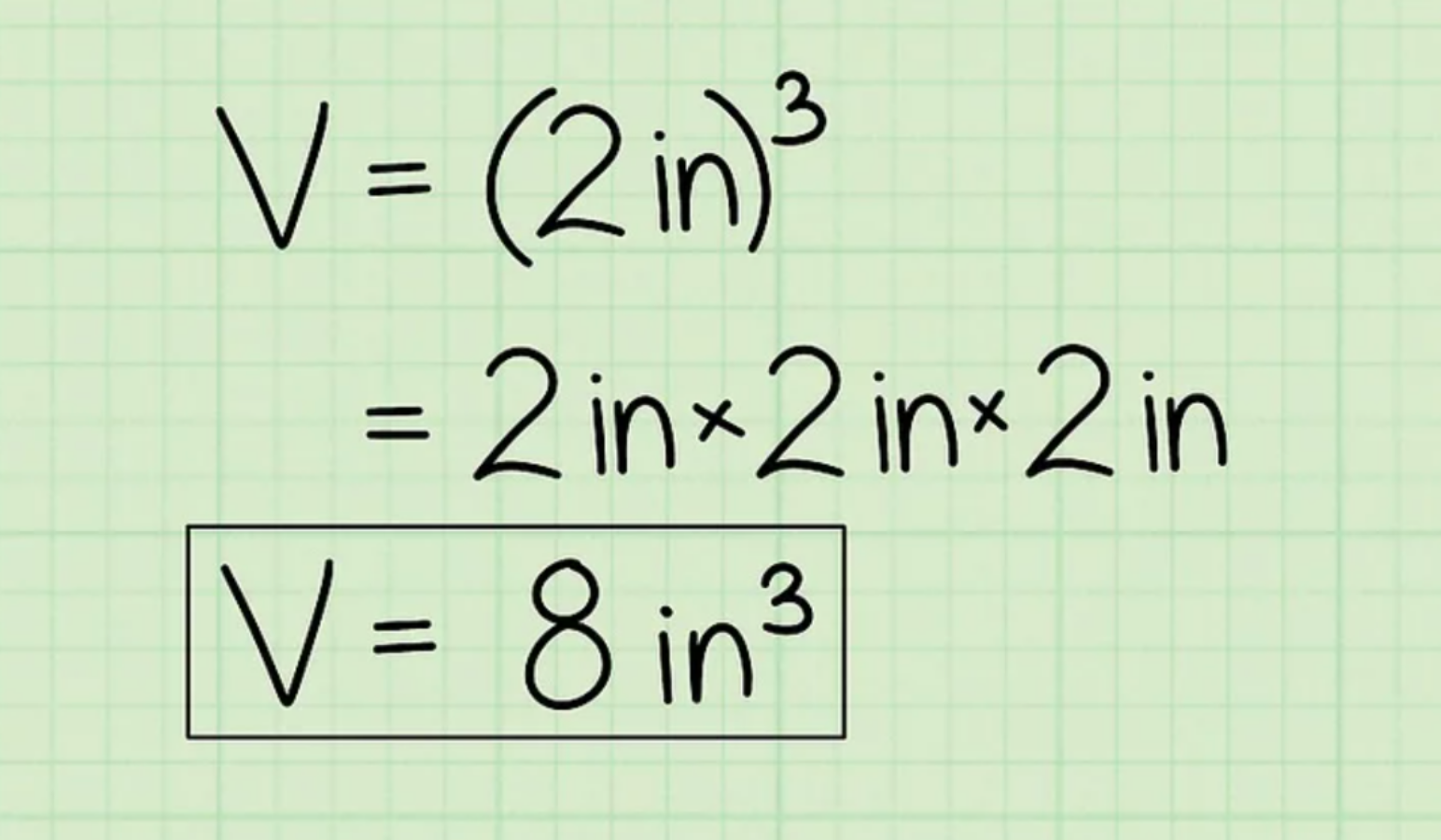
2. Tìm thể tích từ diện tích toàn phần
Bước 1: Tìm diện tích toàn phần của hình lập phương
Trong trường hợp bạn biết diện tích toàn phần của hình lập phương bạn vẫn có thể tìm được thể tích của khối lập phương đó bằng cách chia diện tích toàn phần của hình lập phương cho 6, rồi khai căn bậc 2 của giá trị này để tìm độ dài cạnh hình lập phương. Sau đó, bạn chỉ cần lũy thừa bậc 3 độ dài cạnh để tìm thể tích như bình thường.
Công thức tính diện tích toàn phần của hình lập phương: 6s2 (s là độ dài cạnh hình lập phương).
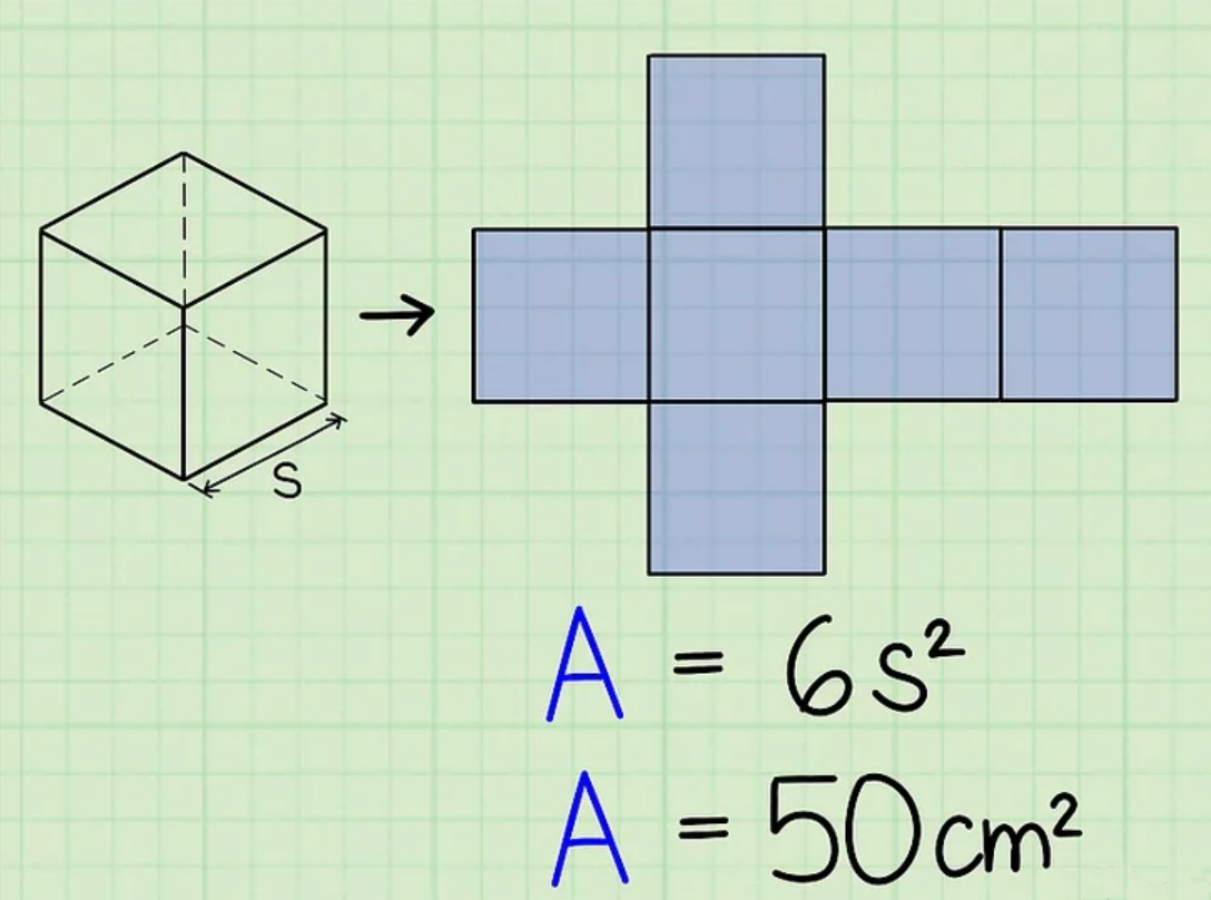
Bước 2: Chia diện tích toàn phần của hình lập phương cho 6
Vì hình lập phương có 6 mặt với diện tích bằng nhau. Vậy nên khi chia diện tích toàn phần của hình lập phương cho 6 sẽ có được giá trị diện tích của 1 mặt. Khi đó, diện tích này bằng tích 2 cạnh 1 mặt hình lập phương (chiều dài × chiều rộng, chiều rộng × chiều cao, hoặc chiều cao × chiều dài).

Bước 3: Tính căn bậc 2 của giá trị này
Vì diện tích 1 mặt hình lập phương bằng s2 (s × s), suy ra căn bậc 2 của giá trị này sẽ cho bạn độ dài cạnh hình lập phương. Khi đó, bạn có thể tính thể tích hình lập phương như bình thường.
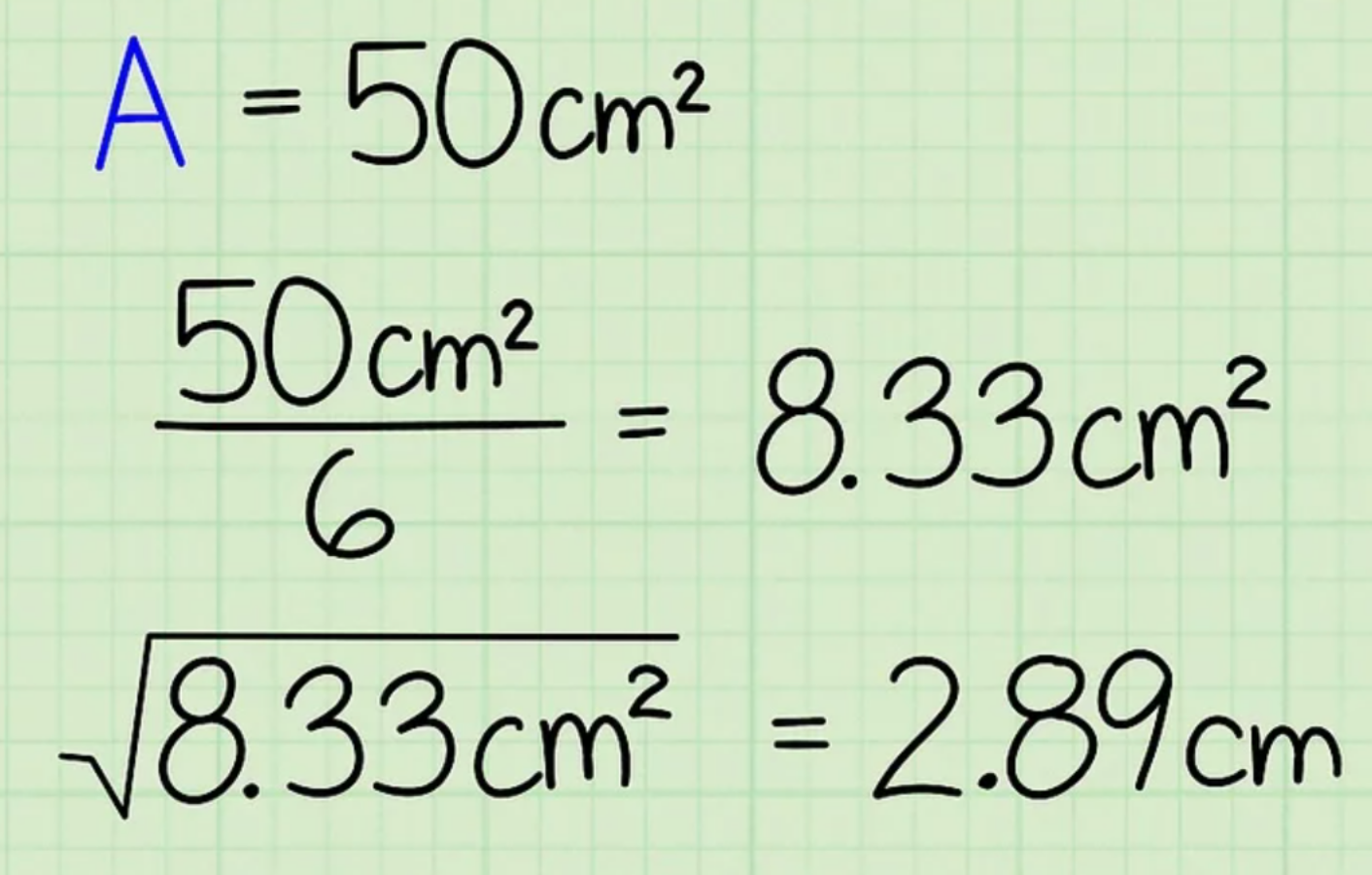
Bước 4: Lũy thừa bậc 3 giá trị này để tìm thể tích hình lập phương
Khi đã có giá trị độ dài cạnh hình lập phương, bạn hãy lũy thừa bậc 3 giá trị này lên để tìm thể tích hình lập phương như trên là xong.
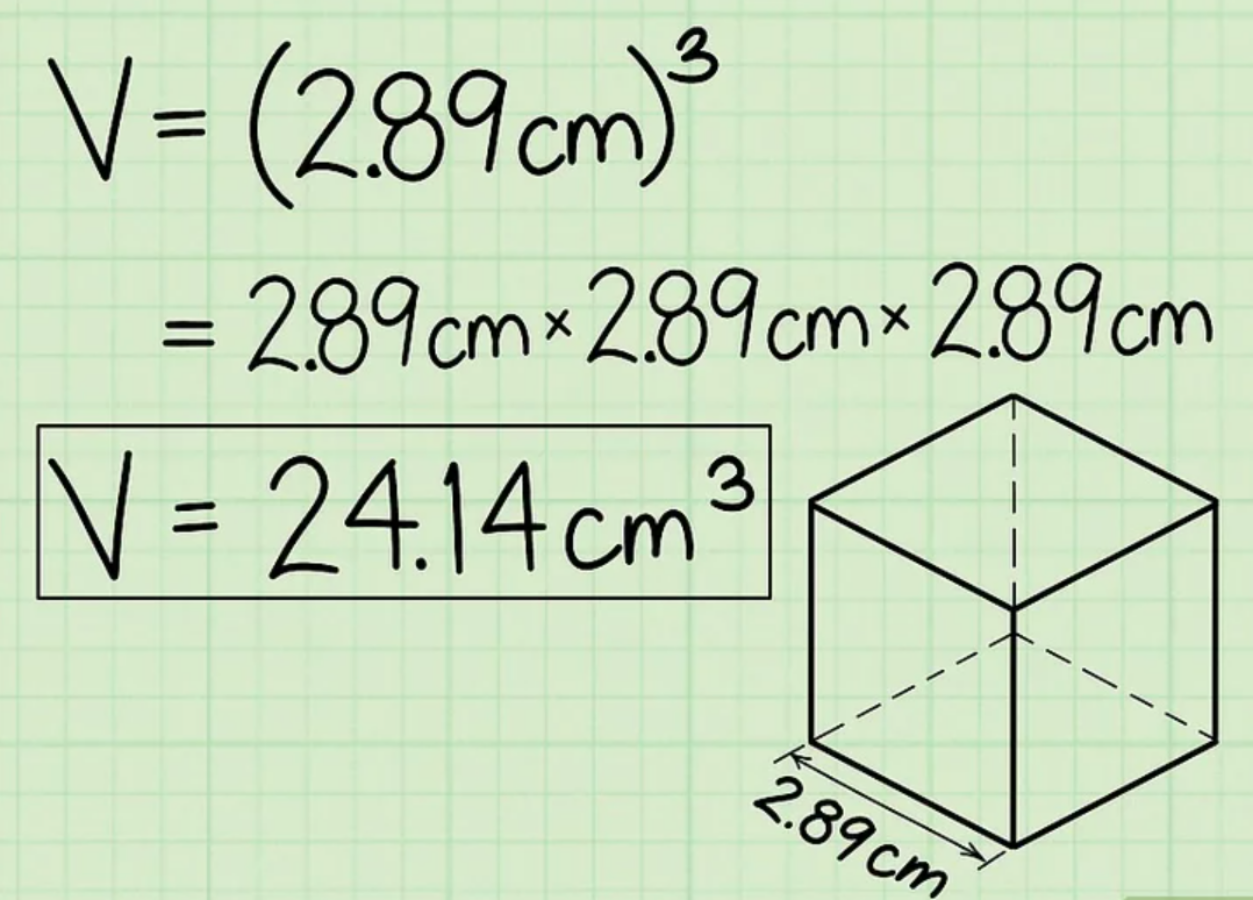
3. Tìm thể tích từ đường chéo
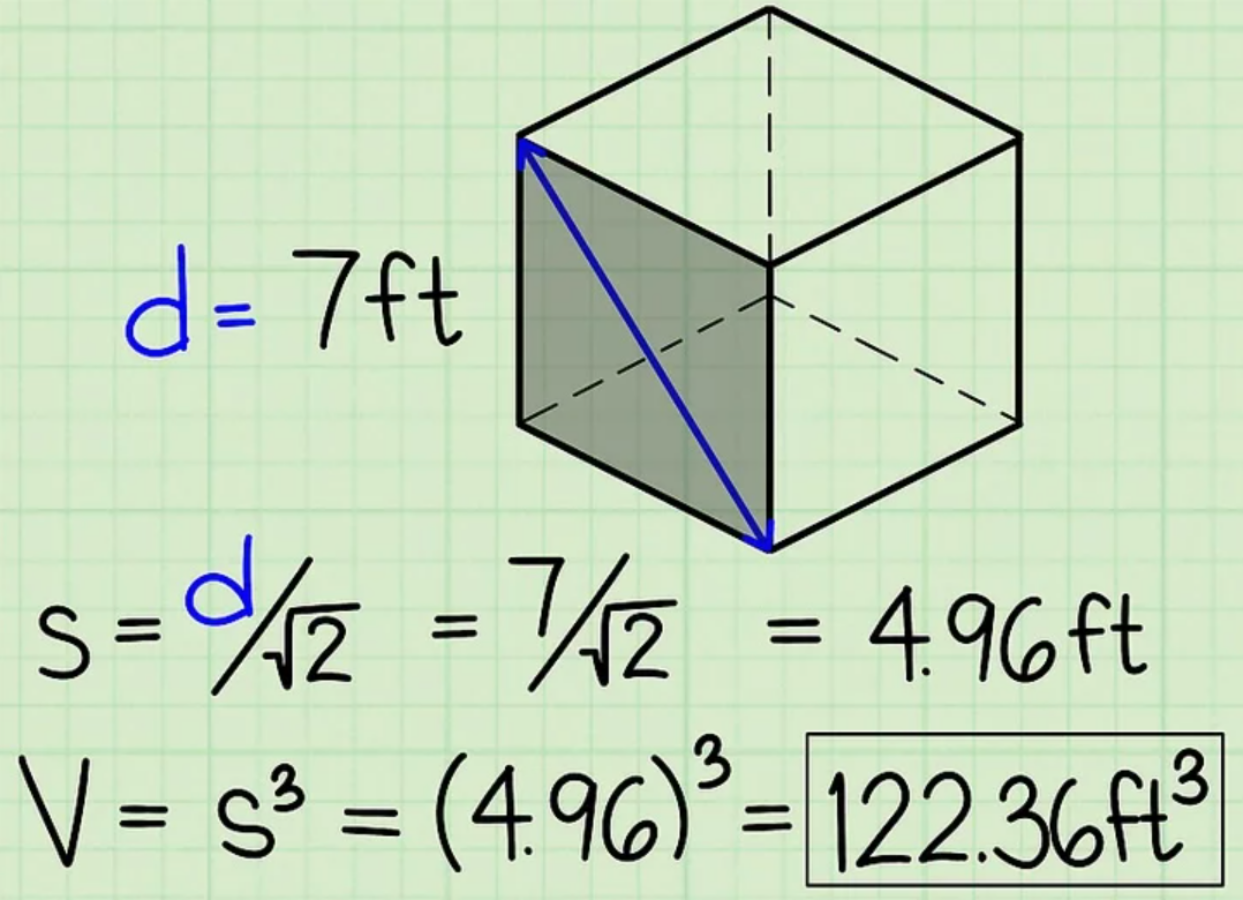
Bước 1: Chia đường chéo của 1 mặt hình lập phương cho √2 để tìm độ dài cạnh hình lập phương
Vì đường chéo của hình vuông bằng √2 × độ dài 1 cạnh hình vuông. Nên nếu bạn có đường chéo 1 mặt hình lập phương, hãy chia cho √2 để tìm độ dài cạnh rồi luỹ thừa bậc 3 để suy ra thể tích hình lập phương
Ví dụ: Cho hình lập phương có độ dài đường chéo là 2,13 m ⇒ Độ dài cạnh hình lập phương: 2,13/√2 = 1,51 m ⇒ Thể tích của hình lập phương là:

Theo công thức tổng quát d2 = 2s2 (d là độ dài đường chéo 1 mặt hình lập phương, s là độ dài cạnh hình lập phương).
Vì theo định lý Pytago, bình phương cạnh huyền của tam giác vuông sẽ bằng tổng bình phương 2 cạnh còn lại. Nên đường chéo của 1 mặt hình lập phương và 2 cạnh vuông của mặt đó tạo ra 1 tam giác vuông ⇒ d2 = s2 + s2 = 2s2.
Bước 2: Bình phương đường chéo kẻ từ 2 điểm đối nhau trên hình lập phương, rồi chia cho 3 và √2 của giá trị tìm được để tìm độ dài cạnh hình lập phương
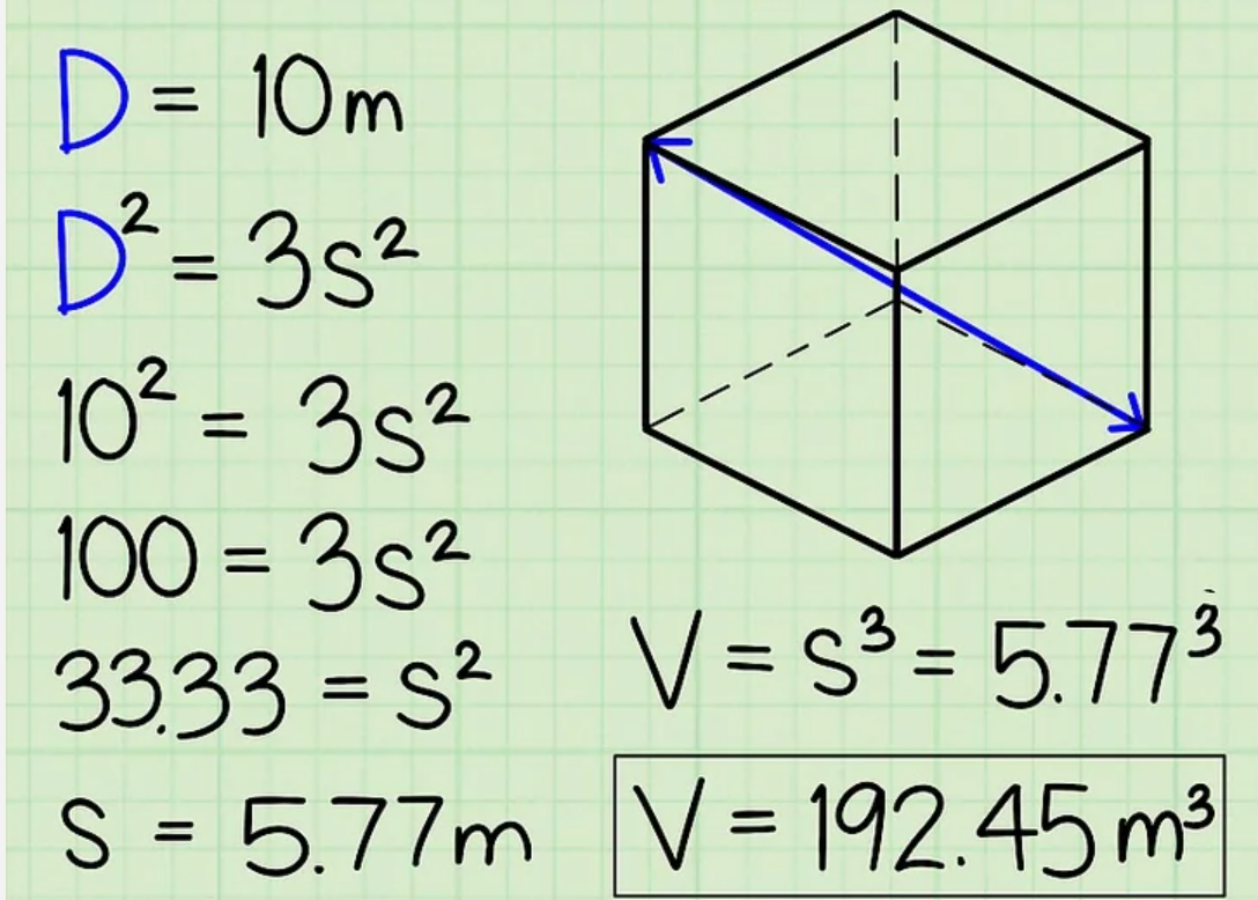
Nếu bạn chỉ có duy nhất dữ liệu về đường chéo kẻ từ góc này của hình lập phương tới góc đối với nó. Khi đó, bạn vẫn có thể tìm được thể tích của hình lập phương bởi D lúc này là 1 cạnh góc vuông của tam giác vuông và cạnh huyền là đường chéo giữa 2 góc của hình lập phương đó. Suy ra, ta có D2 = 3s2.
Theo Định lý Pytago: D, d, và s tạo thành 1 tam giác vuông với D là cạnh huyền, nên ta có D2 = d2 + s2. Như trên, d2 = 2s2 ⇒ D2 = 2s2 + s2 = 3s2.
Ví dụ: Nếu biết độ dài đường chéo từ 1 góc ở mặt đáy hình lập phương tới góc đối diện của nó ở “mặt trên” là 10 m. Bạn sẽ thay giá trị 10 vào “D” trong công thức để tính thể tích hình lập phương như sau:
D2 = 3s2
⇔ 102 = 3s2.
⇔ 100 = 3s2
⇔ 33,33 = s2

Một số bài tập tính thể tích hình lập phương
1. Bài tập tính thể tích hình lập phương có lời giải
Câu 1: Hình lập phương A có cạnh 4 cm. Hình lập phương B có cạnh gấp 2 lần cạnh hình lập phương A. Hỏi thể tích hình lập phương B gấp bao nhiêu lần thể tích hình lập phương A.
Giải:
Cạnh hình lập phương B là: 4 x 2 = 8 (cm)
Thể tích hình lập phương B là: 8 x 8 x 8 = 512 (cm3)
Thể tích hình lập phương A là: 4 x 4 x 4 = 64 (cm3)
Ta có 512 : 64 = 8. Vậy :Thể tích hình lập phương B gấp 8 lần thể tích hình lập phương A.
Có thể nhận xét tổng quát hơn:
Thể tích hình lập phương cạnh a là: V1 = a x a x a
Thể tích hình lập phương cạnh 2a là: V2 = 2a x 2a x 2a = 8 x (a x a x a ) = 8 x V1
Vậy khi cạnh hình lập phương gấp lên 2 lần thì V của nó gấp lên 8 lần.
Câu 2: Một hình lập phương có diện tích toàn phần là 294 cm². Hỏi hình lập phương đó có thể tích bao nhiêu?
Giải:
Diện tích một mặt của hình lập phương là: 294 : 6 = 49cm²
Có 49 = 7 x 7 nên độ dài cạnh của hình lập phương là 7cm
Thể tích của hình lập phương là 7 x 7 x 7 = 343cm³
Câu 3: Phải xếp bao nhiêu hình lập phương nhỏ có cạnh 1cm để được một hình lập phương lớn có diện tích toàn phần là 294dm²
Giải:
Diện tích một mặt hình lập phương lớn là: 294 : 6 = 49dm
Có 49 = 7 x 7 suy ra độ dài cạnh hình vuông lớn là 7dm = 70cm
Thể tích hình lập phương lớn là 70 x 70 x 70 = 343000 cm³
Thể tích hình lập phương nhỏ là 1 x 1 x 1 = 1cm³
Vậy cần 343000 hình lập phương nhỏ
Câu 4: Một khối kim loại hình lập phương có cạnh 1/5 m. Mỗi xăng – ti-mét khối kim nặng 6,2 g. Hỏi khối kim loại đó cân nặng bao nhiêu ki-lô-gam?
Giải: 1/5 m = 20 cm
Thể tích của khối kim loại hình lập phương là: 20 x 20 x 20 = 8000 (cm3)
Khối kim loại đó cân nặng là: 6,2 x 8000 = 49600 (g)
49 600 g = 49,6 kg
Đáp số: 49,6 kg
Câu 5: Một hình lập phương có cạnh 7 cm. Nếu cạnh của hình lập phương tăng lên 4 lần. Hỏi thể tích hình lập phương tăng lên mấy lần?
Giải:
Thể tích ban đầu của hình lập phương là: 7 x 7 x 7 = 343cm²
Thể tích lúc sau của hình lập phương là: 28 x 28 x 28 = 21952cm²
Số lần thể tích tăng lên là: 21952 : 343 = 64 lần
Câu 6: Giải toán lớp 5 trang 122 Viết số đo thích hợp vào chỗ trống:
Hình lập phương (1) (2) (3) (4) Độ dài cạnh 1,5m 5/8 dm Diện tích một mặt 36cm2 Diện tích toàn phần 600dm2 Thể tích
Giải:
Phương pháp giải
Áp dụng các công thức:
– Diện tích 1 mặt của hình lập phương = cạnh × cạnh.
– Diện tích toàn phần của hình lập phương = diện tích một mặt × 6.
– Thể tích của hình lập phương = cạnh × cạnh × cạnh.
Đáp án
+) Hình lập phương (1)
Diện tích một mặt hình lập phương là: 1, 5 x 1, 5 = 2,25m²
Diện tích toàn phần hình lập phương là: 1, 5 x 6 = 13,5m²
Thể tích của hình lập phương là: 1, 5 x 1, 5 x 1,5 = 3,375m³
+) Hình lập phương (2)
Diện tích một mặt hình lập phương là: 5/8 x 5/8 = 25/64 dm2
Diện tích toàn phần hình lập phương là: 5/8 x 6 = 75/32 dm2
Thể tích của hình lập phương là: 5/8 x 5/8 x 5/8 = 125512 dm3 x x
+) Hình lập phương (3):
Vì 36 = 6 × 6 nên cạnh hình lập phương dài 6cm.
Diện tích toàn phần hình lập phương là: 36 × 6 = 216 (cm2)
Thể tích hình lập phương là: 6 × 6 × 6 = 216(cm3)
+) Hình lập phương (4):
Diện tích một mặt hình lập phương là: 600 : 6 = 100 (dm2)
Vì 100 = 10 × 10100 = 10 × 10 nên cạnh hình lập phương dài 10dm.
Thể tích hình lập phương là: 10 × 10 × 10 = 1000(dm3)
Ta có kết quả như sau:
Hình lập phương (1) (2) (3) (4) Độ dài cạnh 1,5m 5/8 dm 6 cm 10 dm Diện tích một mặt 2,25 m2 25/64 dm2 36 cm2 100dm2 Diện tích toàn phần 13,5 m2 75/32 dm2 216cm2 600dm2 Thể tích 3,375 m3 125/512 dm2 216cm3 1000dm3
Câu 7: Một khối kim loại hình lập phương có cạnh là 0,75m. Mỗi đề-xi-mét khối kim loại đó nặng 15 kg. Hỏi khối kim loại đó cân nặng bao nhiêu ki-lô-gam?
Giải:
Thể tích của khối kim loại đó là: 0,75 × 0,75 × 0,75 = 0,421875 (m3)
Ta có: 0,421875 (m3) = 421,875 dm3
Khối kim nặng có cân nặng: 15 x 421,875 = 6328,125 (kg)
Đáp số: 6328,125 (kg)
Câu 8: Một hình hộp chữ nhật có chiều dài 8cm, chiều rộng 7 cm và chiều cao 9cm. Một hình lập phương có cạnh bằng trung bình cộng của ba kích thước của hình hộp chữ nhật trên. Tính:
a) Thể tích của hình hộp chữ nhật
b) Thể tích của hình lập phương
Giải:
a) Thể tích của hình hộp chữ nhật: 8 × 7 × 9 = 504 (cm3)
b) Số đo của hình lập phương là: (8 + 7 + 9) : 2 = 8 (cm)
Thể tích của hình lập phương là: 8 × 8 × 8 = 512 (cm3)
Đáp số: a) 504 cm3
b) 512 cm3
Câu 9: Một hình lập phương có cạnh 2,5 cm. Tính thể tích của hình lập phương đó.
Giải:
Thể tích của hình lập phương là: 2,5 x 2,5 x 2,5 = 15,625 (cm3). Đáp số: 15,625cm3
Câu 10: Diện tích đáy của một bể kính hình hộp chữ nhật là 250cm² và bể đang chứa nước. Biết rằng nếu cho một khối lập phương bằng kim loại cạnh 10cm vào bể (đáy trên khối lập phương bằng mặt nước) thì khối lập phương vừa vặn ngập trong nước . Hãy tính chiều cao mực nước.
Giải:
Tổng thể tích của lượng nước có trong bể và thể tích khối lập phương là: 250 x 10 = 2500 cm³
Thể tích của khối lập phương là: 10 x 10 x 10 = 1000cm³
Thể tích lượng nước có trong bể là: 2500 – 1000 = 1500cm³
Chiều cao mực nước là: 1500 : 250 = 6cm
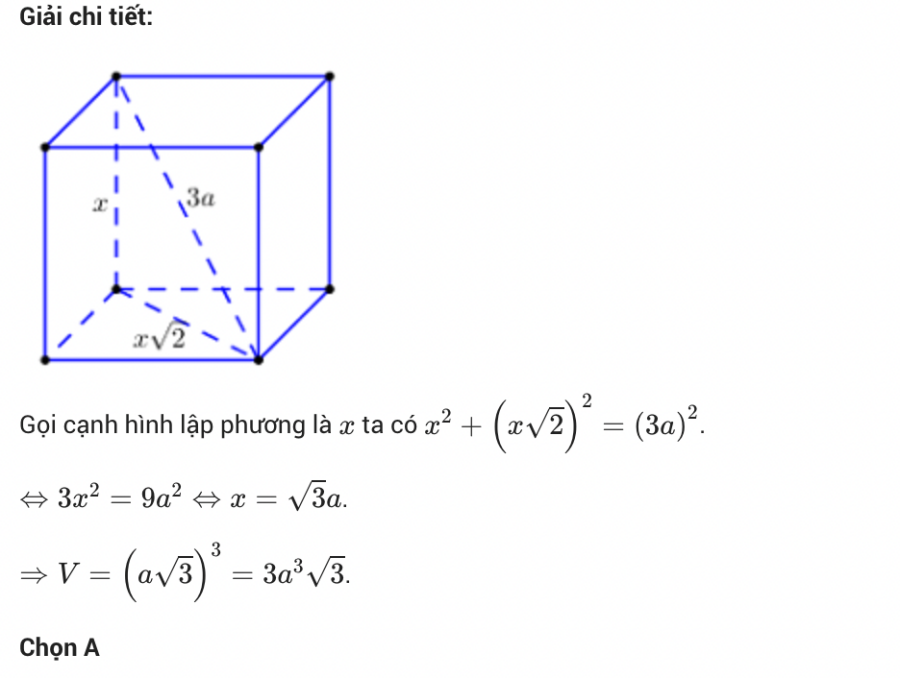
Câu 11: Tính thể tích của khối lập phương có đường chéo bằng 3a?

2. Bài tập tính thể tích hình lập phương không có lời giải
Câu 1: Viết số đo thích hợp với ô trống:
Cạnh của hình lập phương 2,5m 3/4dm 4cm 5dm Thể tích
Câu 2: Tính thể tích hình lập phương cạnh a:
a) a = 6cm
b) a = 7,5 dm
c) a = 4/5 m
Câu 3: Hình lập phương A có cạnh 4 cm. Hình lập phương B có cạnh gấp 2 lần cạnh hình lập phương A. Hỏi thể tích hình lập phương B gấp bao nhiêu lần thể tích hình lập phương A.
Câu 4: Cho một mặt của hình lập phương có đường chéo bằng 3 mét. Tính thể tích của hình lập phương.
Câu 5: Tính thể tích của hình lập phương biết diện tích toàn phần của nó bằng 24 cm2.
Câu 6: Thể tích hình lập phương có cạnh bằng 4dm 2cm là bao nhiêu?
Câu 7: Thể tích của khối lập phương tăng bao nhiêu lần nếu cạnh của khối lập phương đó tăng lên 3 lần?
Câu 8: Một cái bể hình lập phương cạnh 1,5m. Bể không có nước, người ta đổ vào 63 thùng nước, mỗi thùng 25 lít nước. Hỏi mực nước trong bể còn cách miệng bể bao nhiêu mét?
Câu 9: Một cái bể hình lập phương cạnh 1,4m. Bể hiện đang đầy nước, người ta bơm hết nước từ bể này sang một bể thứ hai không có nước hình lập phương có cạnh 2m. Hỏi mực nước trong bể thứ hai còn cách miệng bể bao nhiêu mét?
Câu 10: Một cái thùng hình lập phương cạnh 1,2m. Thùng chứa đầy nước. Người ta bỏ vào thùng một khối sắt hình lập phương cạnh 0,6m thì nước trong thùng trào ra. Hỏi:
a, Số nước trong thùng trào ra là bao nhiêu lít?
b, Sau đó người ta lấy khối sắt ra thì mực nước trong thùng cao bao nhiêu?
3. Thể tích hình lập phương lớp 5 có lời giải
Câu 1: Bài tập 1 trang 122 sách giáo khoa lớp 5
Bài giải:
+) Hình lập phương thứ 1
Ta có:
Ta có diện tích một mặt hình lập phương là: 1,5 x 1,5 = 2,25 (m²)
Ta lại tính được diện tích toàn phần hình lập phương là: 1,5 x 6 = 13,5 (m²)
Ta được, thể tích của hình lập phương là: 1,5 x 1,5 x 1,5 = 3,375 (m³)
+) Hình lập phương thứ 2:
Ta lại có:
Diện tích một mặt hình lập phương là: (dm2)
Diện tích toàn phần hình lập phương là: (dm2)
Thể tích của hình lập phương là: V = (dm3)
+) Hình lập phương thứ 3:
Bởi vì 36 = 6 × 6 nên cạnh hình lập phương dài 6 (cm).
Suy ra: Diện tích toàn phần hình lập phương là: 36 × 6 = 216 (cm2)
Từ đó: Ta tính được thể tích hình lập phương là: 6 × 6 × 6 = 216 (cm3)
+) Hình lập phương thứ 4:
Ta có:
Ta có diện tích một mặt hình lập phương là: 600 : 6 = 100 (dm2)
Ta lại thấy 100 = 10 × 10 nên cạnh hình lập phương dài 10 (dm).
Từ đó ta có thể tính được thể tích hình lập phương là: 10 × 10 × 10 = 1000(dm3)
Câu 2: Bài tập 2 trang 122 sách giáo khoa lớp 5
Bài giải:
Ta có, thể tích của khối kim loại đó là:
V = 0,75 × 0,75 × 0,75 = 0,421875 (m3)
Ta đổi: 0,421875 (m3) = 421,875 dm3
Cân nặng của khối kim loại là:
15 x 421,875 = 6328,125 (kg)
Từ đó ta kết luận được: Cân nặng của khối kim loại là 6328,125 (kg).
Câu 3: Bài 3 trang 122 sách giáo khoa lớp 5
Bài giải:
Câu a: Ta có, thể tích của hình hộp chữ nhật là:
V = 8 × 7 × 9 = 504 (cm3)
Câu b: Số đo của hình lập phương là: (8 + 7 + 9) : 2 = 8 (cm)
Từ đó ta tính được thể tích của hình lập phương là: 8 × 8 × 8 = 512 (cm3)
Đáp số:
Câu a: 504 cm3
Câu b: 512 cm3
Câu 4: Bài tập 1 trang 36 vở bài tập lớp 5
Ta có phương pháp giải:
Dựa vào bảng đơn vị đo diện tích sau đây:

Bài giải:
Câu a: 12ha = 120000 (m2)
5km2 = 5000000 (m2)
Câu b: 2500 dm2 = 25 (m2)
90000 dm2 = 900 (m2)
Câu c: 8m2 26 dm2 = (m2)
45dm2 = (m2)
Câu d: 20m2 4dm2 = (m2)
7m2 7dm2 = (m2)
Câu 5: Bài tập 2 trang 36 vở bài tập lớp 5
Hướng dẫn giải:
Ta thấy: 4cm2 7mm2 > 47mm2
Ta thấy: 2m2 15dm2 = m2
Ta thấy: 5dm2 9cm2 < 590cm2
Ta thấy: 260ha < 26km2
Câu 6: Bài tập 3 trang 37 vở bài tập lớp 5
Hướng dẫn giải:
Chiều rộng của khu rừng là: 3000 × = 1500 m
Diện tích khu rừng đó là: S = 3000× 1500= 4500000 (m2)
Đổi: 4500000 m2 = 450 ha
Đáp số: 45000000 m2; 450 ha.
Câu 6: Bài 4 trang 38 vở bài tập lớp 5
Hướng dẫn giải:
Ta có diện tích căn phòng hình chữ nhật là: 8 × 6 = 48 (m2)
Số tiền mua gạch để lát căn phòng là: 90000 × 48 = 4320000 (đồng)
Đáp số: Số tiền để mua gạch lát kín căn phòng là 4320000 đồng.
4. Thể tích hình lập phương lớp 12 có lời giải
Bài 1: Khối lập phương là khối đa diện đều loại nào sau đây?
A. {3;5}
B. {3;4}
C. {3;3}
D. {4;3}
Hướng dẫn giải:
Cách giải: Dựa vào lí thuyết về khối đa diện đều ta có khối lập phương thuộc loại {4;3}
→ Chọn câu D.
Bài 2: Tính thể tích của khối lập phương có cạnh bằng 4.
A. 64/3
B. 64
C. 16
D. 4
Hướng dẫn giải:
Cách giải: Thể tích của hình lập phương có cạnh bằng 4 là: V = 43 = 64
→ Chọn câu B.
Bài 3: Cho khối lập phương ABCD.A’B’C’D’ có O và O’ lần lượt là tâm các hình vuông ABCD và A’B’C’D’. Gọi V1 là thể tích khối nón tròn xoay có đỉnh là trung điểm của OO’ và đáy là đường tròn ngoại tiếp hình vuông A’B’C’D’, V2 là thể tích khối trụ tròn xoay có hai đáy là hai đường tròn nội tiếp hai hình vuông ABCD và A’B’C’D’. Tỷ số thể tích V1/V2 là:
A. 1/2
B. 1/4
C. 1/6
D. 1/3
Cách giải:
Giả sử cạnh hình vuông bằng a.
Khối nón có chiều cao
h1 = a/2, bán kính đáy r1 = (a√2)/2
V1 = π/3 . ((a√2)/2)^2 . a/2 = (πa^3)6
Khối trụ có chiều cao h2 = a, bán kính đáy r2 = a/2
=> V2 = π (a/2)^2. a = π.a^3/2
=> V1/V2 = 1/3
-> Chọn câu D.
Trên đây là công thức Thể tích hình lập phương & cách tính thể tích hình lập phương & đơn giản, nhanh chóng mà đội ngũ INVERT chúng tôi đã tổng hợp được. Mong rằng thông qua bài viết này các bạn hoàn toàn có thể tính được thể tích hình lập phương một cách dễ dàng.
Chào mừng bạn đến với PRAIM, - nền tảng thông tin, hướng dẫn và kiến thức toàn diện hàng đầu! Chúng tôi cam kết mang đến cho bạn một trải nghiệm sâu sắc và tuyệt vời về kiến thức và cuộc sống. Với Praim, bạn sẽ luôn được cập nhật với những xu hướng, tin tức và kiến thức mới nhất.

















