Số Mũ Trong Tiếng Anh: Tìm Hiểu Khái Niệm Và Tính Chất

Đã bao giờ bạn tự hỏi về lũy thừa số mũ trong toán học? Lũy thừa không chỉ là một phần cơ bản của toán học mà còn có rất nhiều ứng dụng thực tế, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về lũy thừa số mũ trong toán tiếng Anh, từ những định nghĩa cơ bản cho đến các tính chất và ví dụ cụ thể.

Khái niệm Lũy thừa số mũ trong toán tiếng Anh

Lũy thừa số mũ là một khái niệm không thể thiếu trong toán học và thường xuất hiện trong nhiều dạng bài toán khác nhau. Nhưng bạn có hiểu rõ về khái niệm này không?

Lũy thừa số mũ đơn giản là khi một số được nhân lên với chính nó để biểu thị sự tăng lên của một giá trị trong toán học. Ví dụ, 6^2 có nghĩa là 6 được nhân lên với chính nó hai lần.

Trong tiếng Anh, có nhiều từ khác nhau để chỉ các khái niệm liên quan đến lũy thừa số mũ như:

• Exponent: chỉ số mũ trong lũy thừa
• Power: chỉ kết quả của phép tính lũy thừa
• Ví dụ: 4^3, kết quả là “power of four to the third”
• Base: dùng để chỉ cơ số trong lũy thừa.

Các tính chất của lũy thừa

Để hiểu rõ về các loại lũy thừa cụ thể, chúng ta cần biết về các tính chất cơ bản của lũy thừa số mũ trong toán tiếng Anh. Dưới đây là một số tính chất quan trọng:

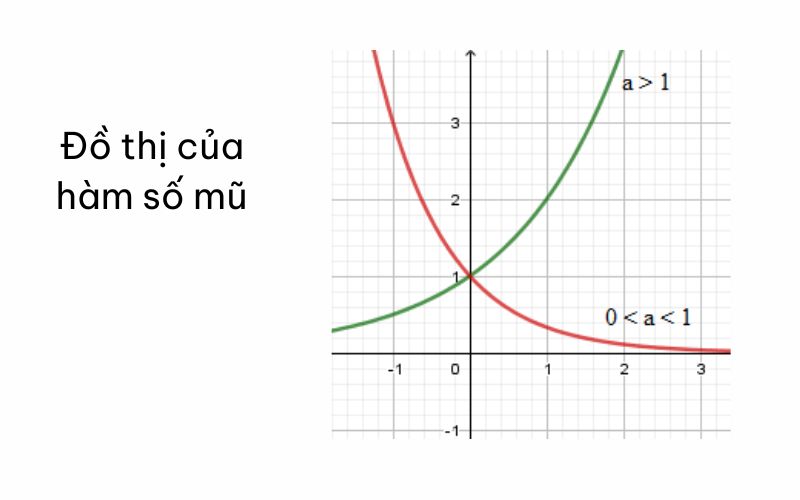
• Trường hợp a > 1, ta có a^α > a^β ⇔ α > β.
• Trường hợp 0 < a < 1, ta có a^α > a^β ⇔ α < β.
• Với trường hợp mọi 0 < a < b, ta có a^m < b^m ⇔ m > 0; a^m > b^m ⇔ m < 0.

Xem thêm: X intercept là gì? Các nội dung toán về x intercept.

Các loại lũy thừa số mũ và ví dụ

Thông qua lũy thừa số mũ, chúng ta có thể tạo ra nhiều loại lũy thừa khác nhau, tùy thuộc vào số được sử dụng làm số mũ. Dưới đây là một số dạng lũy thừa số mũ cơ bản mà bạn cần nắm vững:

Toán lũy thừa với số mũ tự nhiên (Integer exponents)

Số mũ tự nhiên là số nguyên không âm như 2^3, 5^4,… Đây là các loại lũy thừa quen thuộc và thường gặp trong toán học.

Áp dụng tính chất của lũy thừa số mũ, khi nhân hoặc chia số cùng là số mũ tự nhiên có cùng cơ số, ta cần cộng hoặc trừ các số mũ và giữ nguyên cơ số.

Ví dụ:

• 2^3 + 2^4 = 2^(3+4) = 2^7
• 2^3 / 2^2 = 2^(3-2) = 2^1

Lưu ý: Các tính chất này cũng có thể áp dụng với các số mũ tự nhiên âm.

Lũy thừa của số thực dương với số mũ hữu tỷ (Rational exponents)

Số mũ hữu tỷ là một phân số có dạng a/b, trong đó a và b là số nguyên và b khác 0. Ví dụ: 3^½, 4^⅔ , …. đều là các số mũ hữu tỷ.

Lũy thừa với số mũ thực (Real exponents)

Số mũ thực là một số không phải là số nguyên hoặc số hữu tỷ. Ví dụ: 2^π, 10^√2,… đều là các số mũ thực.

Khi có số mũ thực, ta cần sử dụng bảng giá trị để tính.

Ví dụ: 2^π = 8.824977827076287
10^√2 = 14.86927456343641

Lũy thừa với số mũ phức (Complex exponents with a positive real base)

Số mũ phức có dạng a+bi, trong đó a và b là các số thực, i là một số ảo. Khi gặp số mũ phức, chúng ta cần sử dụng khái niệm của hàm số để tính toán.

Ví dụ:
2^(3+2i) = 2^3 x 2^(2i)
= 8 x (cos(2log2) + i.sin(2log2))
= 8(cos0.6135 + i.sin0.6135)
= 8.93731141368623 + 3.85373803749222i

Hàm số lũy thừa (Power function)

Hàm số lũy thừa có dạng f(x) = a^x, trong đó a là cơ sở, x là số mũ. Các tính chất của lũy thừa số mũ cũng có thể áp dụng cho các hàm số lũy thừa.

Ví dụ: f(x) = 3^x, g(x) = 2^x.

Hàm số mũ (Exponential function)

Hàm số mũ cũng có dạng f(x) = a^x, trong đó a là cơ sở, x là số mũ. Tuy nhiên, hàm số mũ khác với hàm số lũy thừa ở chỗ cơ sở a có thể là bất kỳ số thực dương nào, không chỉ là các số tự nhiên.

Hàm số mũ có rất nhiều ứng dụng trong thực tế như: kinh tế học, khoa học máy tính,… Ví dụ: Hàm số lũy thừa được sử dụng để miêu tả quá trình tăng trưởng dân số, phân tích thu nhập bình quân.

Tổng kết

Lũy thừa số mũ trong toán tiếng Anh là một khái niệm cơ bản và rất quan trọng khi học sinh theo học các hệ quốc tế. Việc hiểu rõ về lũy thừa số mũ giúp học sinh áp dụng chúng một cách chính xác và hiệu quả. Hy vọng với những thông tin mà PRAIM đã chia sẻ ở trên đã giúp bạn có thêm hiểu biết về phần học này.