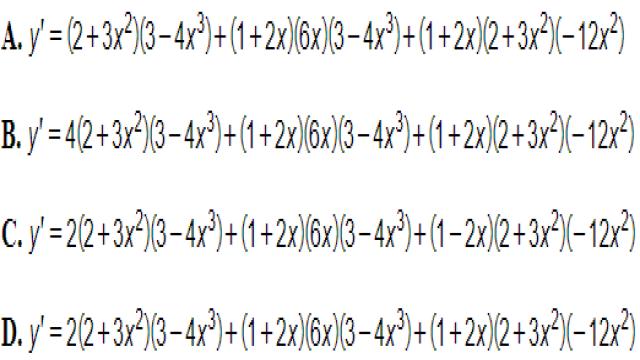Lý thuyết Toán 11 Bài 2: Quy tắc tính đạo hàm
Bài giảng Toán 11 Bài 2: Quy tắc tính đạo hàm
A. LÝ THUYẾT
I. Đạo hàm của một hàm số thường gặp
1. Định lí 1
Hàm số y = xn có đạo hàm tại mọi x∈ℝ và (xn)’ = n.xn-1.
2. Định lí 2
Hàm số y=x có đạo hàm tại mọi x dương và x’=12x.
Ví dụ 1.
a) Tính đạo hàm y = x3;
b) Tính đạo hàm y=x tại x = 5.
Lời giải
a) Ta có: y’ = 3×2;
b) Ta có: y’=12x
Đạo hàm của hàm số tại x = 5 là: y’5=125.
II. Đạo hàm của tổng, hiệu, tích, thương
1. Định lí 3
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định, ta có:
(u + v)’ = u’ + v’;
(u – v)’ = u’ – v’;
(uv)’ = u’.v + u.v’;
uv’=u’v−u.v’v2v=v(x)≠0.
2. Hệ quả
Hệ quả 1. Nếu k là một hằng số thì (ku)’ = k.u’.
Hệ quả 2. 1v’=−v’v2.
Ví dụ 2. Tính đạo hàm của các hàm số sau:
a) y = x5 – 2×2 + 3x + 6;
b) y = (x2 + 1)(2x – 3);
c) y=7x2x−1.
Lời giải
a) y = x5 – 2×2 + 3x
⇒y’ = (x5 – 2×2 + 3x)’
= (x5)’ – (2×2)’ + (3x)’
= 5×4 – 4x + 3.
b) y = (x2 + x).2x
⇒y’ = (x2 + x)’.2x + (x2 + 1)(2x)’
= [(x2)’ + x’].2x + (x2 + 1).2
= (2x + 1).2x + 2×2 + 2
= 4×2 + 2x + 2×2 + 2
= 6×2 + 2x + 2.
c)
y=7x2x−1⇒y=7×2’x3−2x−7x2x3−2x’x3−2×2=14xx3−2x−7x22x2−2×3−2×2=14×4−28×2−14×2+14xx3−2×2=−28×2+14xx3−2×2
III. Đạo hàm hàm hợp
Định lý 4. Nếu hàm số u = g(x) có đạo hàm x là và hàm số y = f(u) có đạo hàm tại u là thì hàm hợp y = f(g(x)) có đạo hàm tại x là: yx’=yu’.ux’.
Ví dụ 3. Tính đạo hàm của hàm số: y=x2+2x
Lời giải
Đặt u=x2+2x thì y=u
y’=u’2u=x2+2x’2×2+2x=2x+22×2+2x.
B. BÀI TẬP
Bài 1. Tính đạo hàm các hàm số sau:
1. y=x3−3×2+2x+1
2. y=−x3+3x+1
3. y=x44−x2+1
4. y=−2×4+32×2+1
5. y=2x+1x−3
6. y=x2−2x+2x+1
Lời giải
1. Ta có: y’=−x3+3x+1’=3×2−6x+2
2. Ta có: y’=−x3+3x+1’=−3×2+3
3. Ta có: y’=x44−x2+1’=x3−2x
4. Ta có: y’=−2×4+32×2+1’=−8×3+3x
5. Ta có:
y’=(2x+1)'(x−3)−(x−3)'(2x+1)(x−3)2=−7(x−3)2
6. Ta có:
y’=(x2−2x+2)'(x+1)−(x2−2x+2)(x+1)'(x+1)2=(2x−2)(x+1)−(x2−2x+2)(x+1)2=x2+2x−4x+12
Bài 2. Tính đạo hàm các hàm số sau:
a) y=x7+x2
b) y=2×2+3x+1
Lời giải
a) Đặt u = (x7 + x)2
⇒y’u=2×7+xx7+x’=2×7+x7x+1
b) Đặt u = 2×2 + 3x + 1
⇒y’u=u’2u=2×2+3x+1’22×2+3x+1=4x+322×2+3x+1
Bài 3. Cho f(x)=2×3−x2+32 và g(x)=x33+x22+103. Giải bất phương trình f’(x) > g’(x).
Lời giải
Ta có:
f'(x)=2×3−x2+32’=6×2−2xg'(x)=x33+x22+103’=x2+x
Xét bất phương trình: f’(x) > g’(x)
⇔6×2−2x>x2+x⇔5×2−3x>0⇔x<0x>35
Vậy tập nghiệm của bất phương trình là: −∞;0∪35;+∞.
Bài 4. Cho f(x) = x5 + x3 – 2x – 3. Chứng minh rằng:
f’(1) + f’(-1) = -4f(0).
Lời giải
Ta có: f’(x) = (x5 + x3 – 2x – 3)’ = 5×4 + 3×2 – 2.
Khi đó:
f’(1) = 5.14 + 3.12 – 2 = 5 + 3 – 2 = 6.
f’(-1) = 5.(-1)4 + 3.(-1)2 – 2 = 5 + 3 – 2 = 6.
f(0) = 05 + 03 – 2.0 – 3 = 0 + 0 – 0 – 3 = – 3.
f’(1) + f’(-1) = 6 + 6 = 12 và -4f(0) = -4.(-3) = 12.
Vậy f’(1) + f’(-1) = -4f(0).
Trắc nghiệm Toán 11 Bài 2: Quy tắc tính đạo hàm
Câu 1: Cho hàm số y=x2+xx−2 đạo hàm của hàm số tại x=1 là:
A. y’1=−4
B. y’1=−5
C. y’1=−3
D. y’1=−2
Câu 2: Tính đạo hàm của hàm số sau:
y=x4−3×2+2x−1
A. y’=4×3−6x+3
B. y’=4×4−6x+2
C. y’=4×3−3x+2
D. y’=4×3−6x+2
Câu 3. Tính đạo hàm của hàm số y=1−2×2.
A. y’=121−2×2.
B. y’=−4×1−2×2.
C. y’=−2×1−2×2.
D. y’=2×1−2×2.
Câu 4: Tính đạo hàm của hàm số fx=−x4+4×3−3×2+2x+1 tại điểm x=−1.
A. f’−1=4.
B. f’−1=14.
C. f’−1=15.
D. f’−1=24.
Câu 5: Cho hàm số fx xác định trên R bởi f(x)=x2. Giá trị f'(0) bằng
A. 0.
B. 2
C. 1
D. Không tồn tại
Câu 6: Tính đạo hàm của hàm số sau fx=x2−3x+1 khi x>12x+2 khi x≤1 ta được:
A. f'(x)=2x−3 khi x>12 khi x≤1
B. f'(x)=2x−3 khi x>12 khi x<1
C. Không tồn tại đạo hàm
D. f’x=2x−3
Câu 7. Đạo hàm của hàm số y=(x3−2×2)2016 là:
A. y’=2016(x3−2×2)2015.
B. y’=2016(x3−2×2)2015(3×2−4x).
C. y’=2016(x3−2×2)(3×2−4x).
D. y’=2016(x3−2×2)(3×2−2x).
Câu 8. Tính đạo hàm của hàm số sau: y=1+2×2+3×23−4×3
Câu 9. Tính đạo hàm của hàm số y=(x+1)x2+x+1.
A. 4×2−5x+32×2+x+1
B. 4×2+5x−32×2+x+1
C. 4×2+5x+3×2+x+1
D. 4×2+5x+32×2+x+1
Câu 10: Đạo hàm cấp một của hàm số y=1−x35 là:
A. y’=51−x34
B. y’=−15×21−x34
C. y’=−31−x34
D. y’=−5×21−x34
Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:
Lý thuyết Ôn tập chương 4
Lý thuyết Định nghĩa và ý nghĩa của đạo hàm
Lý thuyết Đạo hàm của hàm số lượng giác
Lý thuyết Đạo hàm cấp hai
Lý thuyết Ôn tập chương 5
Chào mừng bạn đến với PRAIM, - nền tảng thông tin, hướng dẫn và kiến thức toàn diện hàng đầu! Chúng tôi cam kết mang đến cho bạn một trải nghiệm sâu sắc và tuyệt vời về kiến thức và cuộc sống. Với Praim, bạn sẽ luôn được cập nhật với những xu hướng, tin tức và kiến thức mới nhất.