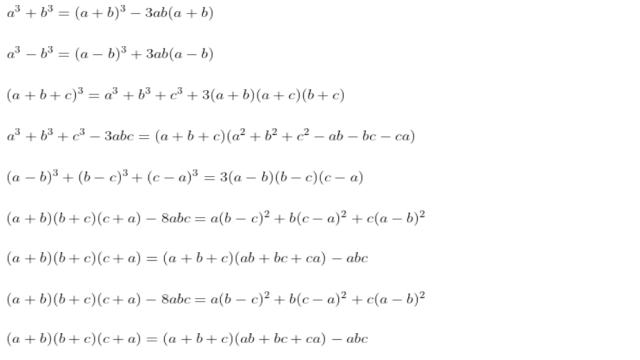7 Hằng Đẳng Thức Đáng Nhớ: Bí Quyết Ghi Nhớ Dễ Dàng

Giới thiệu: Hằng đẳng thức là “nỗi ám ảnh” của một số học sinh lớp 7, lớp 8. Tuy nhiên, việc nhớ các hằng đẳng thức không khó như chúng ta nghĩ. Chỉ cần mài dũa và làm bài tập thường xuyên, bạn đã có thể thuần thục 7 hằng đẳng thức đáng nhớ. Hãy cùng PRAIM tìm hiểu chi tiết về chủ đề thú vị này.

1. 7 Hằng đẳng thức đáng nhớ là gì?

Trong toán học, hằng đẳng thức là một loạt các đẳng thức có liên quan tới nhau hợp lại tạo thành một hằng đẳng thức. Các hằng đẳng thức này được sử dụng phổ biến trong các bài toán phân tích đa thức của học sinh cấp II và cấp III. Việc thuộc lòng các hằng đẳng thức sẽ giúp bạn giải nhanh những bài toán khó hơn.

2. Công thức 7 hằng đẳng thức đáng nhớ

Có 7 công thức đáng nhớ sau:

1. Bình phương của một tổng: ( A + B )^2 = A^2 + 2AB + B^2.
2. Bình phương của một hiệu: ( A – B )^2 = A^2 – 2AB + B^2.
3. Hiệu của hai bình phương: A^2 – B^2 = ( A – B )( A + B ).
4. Lập phương của một tổng: ( A + B )^3 = A^3 + 3A^2B + 3AB^2 + B^3.
5. Lập phương của một hiệu: ( A – B )^3 = A^3 – 3A^2B + 3AB^2 – B^3.
6. Tổng của hai lập phương: A^3 + B^3 = ( A + B )( A^2 – AB + B^2 ).
7. Hiệu của hai lập phương: A^3 – B^3 = ( A – B )( A^2 + AB + B^2 ).

3. Một số hệ quả

Một số hệ quả với các hằng đẳng thức đáng nhớ dạng bậc 2:

4. Phát biểu 7 hằng đẳng thức đáng nhớ bằng lời cực đơn giản

1. Bình phương của 1 tổng: Bình phương của 1 tổng bằng bình phương của số thứ nhất cộng với 2 lần tích của số thứ nhất nhân với số thứ hai, rồi cộng với bình phương của số thứ hai.
2. Bình phương của 1 hiệu: Bình phương của 1 hiệu bằng bình phương của số thứ nhất trừ đi 2 lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương của số thứ hai.
3. Hiệu hai bình phương: Hiệu hai bình phương của hai số bằng tổng hai số đó nhân với hiệu hai số đó.
4. Lập phương của 1 tổng: Lập phương của 1 tổng hai số bằng lập phương của số thứ nhất cộng với 3 lần tích bình phương số thứ nhất nhân số thứ hai, sau đó cộng với 3 lần tích số thứ nhất nhân với bình phương số thứ hai, và cuối cùng cộng với lập phương số thứ hai.
5. Lập phương của 1 hiệu: Lập phương của 1 hiệu hai số bằng lập phương của số thứ nhất trừ đi 3 lần tích bình phương của số thứ nhất nhân với số thứ hai, sau đó cộng với 3 lần tích số thứ nhất nhân với bình phương số thứ hai, và cuối cùng trừ đi lập phương số thứ hai.
6. Tổng hai lập phương: Tổng của hai lập phương hai số bằng tổng của hai số đó nhân với bình phương thiếu của hiệu hai số đó.
7. Hiệu hai lập phương: Hiệu của hai lập phương hai số bằng hiệu hai số đó nhân với bình phương thiếu của tổng của hai số đó.

5. Mẹo ghi nhớ hiệu quả

Để ghi nhớ hiệu quả các hằng đẳng thức, bạn có thể áp dụng các mẹo sau:

• Lưu ý rằng hằng đẳng thức số 1 và 2, 4 và 5, 6 và 7 khá tương tự nhau và chỉ khác nhau một chút về dấu. Vì vậy, thay vì học cả 7, bạn chỉ cần học 4 và lưu nhớ thêm dấu của chúng.
• Theo dõi bài hát “7 Hằng Đẳng Thức Đáng Nhớ” của “Nhật Anh sáng tạo” dựa trên nền nhạc của bài “Sau Tất Cả”. Cách học này sẽ giúp bạn thư giãn hơn và học hiệu quả hơn.

6. Một số bài tập có đáp án

1. Tìm giá trị của x biết: x^2( x – 3) – 4x + 12 = 0.
2. Tính giá trị nhỏ nhất của biểu thức: B = x^2 – 6x + 15.
3. Rút gọn biểu thức sau: C = 4x^2 – 28x + 55.
4. So sánh: A = 1989.1991 và B = 1990^2.

7. Kết luận

Trên đây là những chia sẻ của PRAIM về 7 hằng đẳng thức đáng nhớ. Chúng tôi đã cung cấp các công thức, hệ quả và phát biểu bằng lời của các công thức này. Ngoài ra, cuối bài còn có một số bài tập để bạn thực hành và nâng cao kiến thức của mình. Hãy cùng PRAIM khám phá thêm nhiều kiến thức bổ ích khác tại PRAIM.